 Giải bởi Vietjack
Giải bởi Vietjack
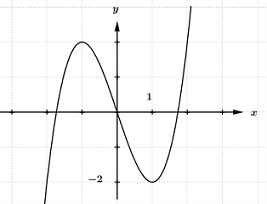
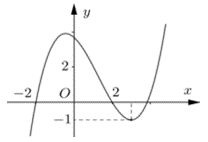
Bước 1: Đặt quan sát đồ thị tìm nghiệm của phương trình tìm các nghiệm ti.
Ta có :
Đặt ta được
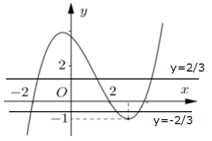
+) Phương trình có ba nghiệm phân biệt trong đó
+) Phương trình có ba nghiệm phân biệt trong đó
Các nghiệm
Bước 2: Khảo sát hàm số suy ra số nghiệm của phương trình
Xét hàm có
BBT :
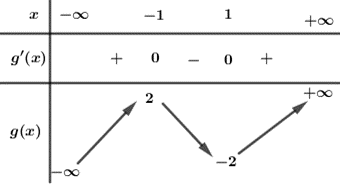
Từ BBT ta thấy :
+) Phương trình có 3 nghiệm phân biệt.
+) Phương trình có 3 nghiệm phân biệt.
+) Phương trình có đúng 1 nghiệm.
+) Phương trình có đúng 1 nghiệm.
+) Phương trình có đúng 1 nghiệm.
+) Phương trình có đúng 1 nghiệm.
Vậy phương trình đã cho có tất cả nghiệm.
Cho hàm số . Giá trị của tham số m để đường thẳng cắt tại ba điểm phân biệt sao cho tam giác KBC có diện tích bằng với điểm là:
Cho hàm số f(x) có bảng biến thiên như sau:
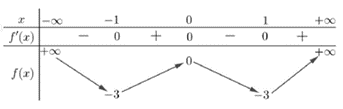
Phương trình có bao nhiêu nghiệm thực?
Cho hàm số liên tục trên và có đồ thị như hình vẽ bên. Số nghiệm của phương trình là:
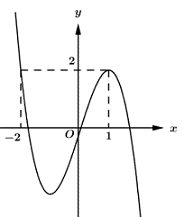
Tìm điều kiện của m để đồ thị hàm số cắt trục hoành tại 4 điểm phân biệt.
Cho hàm số xác định trên liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:
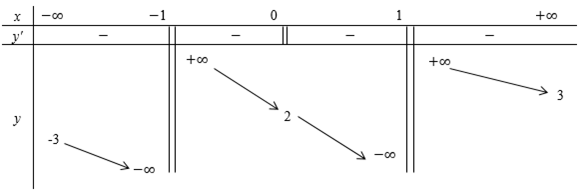
Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt.
Có tất cả bao nhiêu giá trị nguyên thuộc đoạn của tham số m để đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt?
Cho hàm số liên tục trên R và có bảng biến thiên như hình vẽ
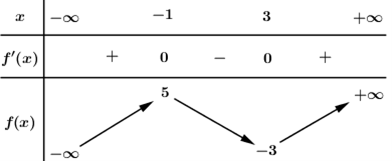
Phương trình có bao nhiêu nghiệm?
Đề thi THPT QG - 2021 - mã 101
Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng
Cho hàm số có bảng biến thiên:
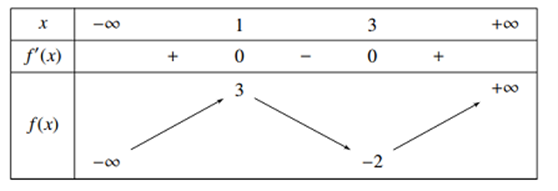
Tìm tất cả các giá trị của mm để bất phương trình vô nghiệm?
Tìm m để đồ thị hàm số cắt đường thẳng tại ba điểm phân biệt có hoành độ thỏa mãn
Cho hàm số liên tục trên có bảng biến thiên như hình vẽ:
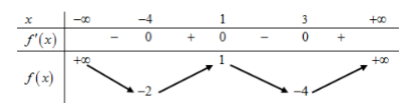
Số nghiệm của phương trình là:
Cho hai đồ thị hàm số và đồ thị hàm số có tất cả bao nhiêu điểm chung?
Cho hàm số có đồ thị (C).Để đồ thị (C) cắt trục hoành tại ba điểm A,B,C sao cho C là trung điểm của AB thì giá trị của tham số m là:
Cho hàm số có đồ thị như hình vẽ. Với các giá trị nào của tham số m thì phương trình có bốn nghiệm phân biệt.