Cho hình thang vuông ABCD, có . Kẻ BH vuông góc với CD.
Gọi M là trung điểm của BH. Chứng minh A đối xứng với C qua M.
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp
Chứng minh ABCH là hình bình hành suy ra M là trung điểm AC.
Cách giải:
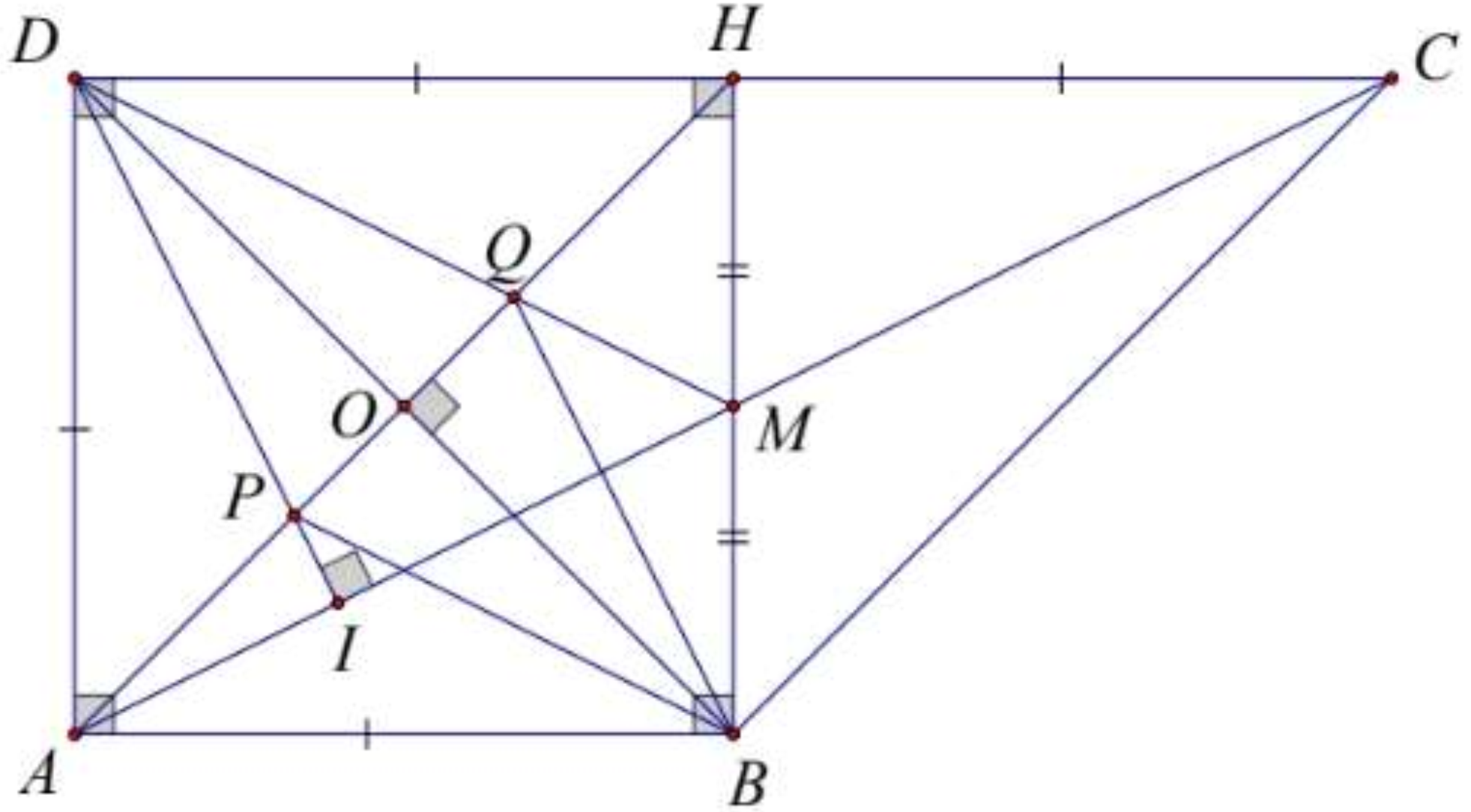
Gọi M là trung điểm của BH. Chứng minh A đối xứng với C qua M.
Ta có: là hình bình hình (dhnb)
Mà M là trung điểm của BH nên M là trung điểm của AC (t/c)
Suy ra A đối xứng với C qua M.
Tam giác ABC có M, N lần lượt là trung điểm của AB, AC, biết , độ dài cạnh BC bằng:
Cho biểu thức với .
Tìm giá trị x nguyên để A nhận giá trị nguyên.
Cho hình thang vuông ABCD, có . Kẻ BH vuông góc với CD.
Kẻ DI vuông góc với AC, DI, DM cắt AH lần lượt tại P và Q. Chứng minh .
Cho hình thang vuông ABCD, có . Kẻ BH vuông góc với CD.
Chứng minh rằng tứ giác ABHD là hình vuông.