Giải bởi Vietjack
Phương pháp:
Chứng minh tứ giác có một cặp cạnh đối vừa song song vừa bằng nhau là hình bình hành.
Cách giải:
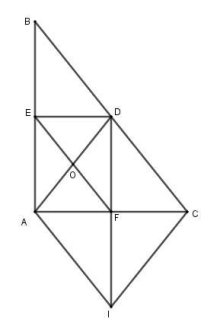
Gọi là giao điểm của và . Chứng minh tứ giác là hình bình hành và từ đó suy ra ba điểm thẳng hàng.
Ta có: nên (từ vuông góc đến song song)
Mà là trung điểm nên là trung điểm
là đường trung bình của tam giác
Mà (do đối xứng với qua )
Do đó .
Mà nên tứ giác là hình bình hành (dhnb).
Vì là giao điểm của với nên là trung điểm .
Tứ giác là hình bình hành hai đường chéo cắt nhau tại là trung điểm của mỗi đường.
Vậy thẳng hàng.
Diện tích hình chữ nhật sẽ thay đổi như thế nào nếu chiều dài tăng 6 lần, chiều rộng giảm 2 lần?
