22 câu hỏi trắc nghiệm thuộc Bộ 14 đề thi Học kì 1 Toán 8 có đáp án - Đề 4

Câu 1:

Phân thức đối của $\frac{2 x - 1}{5 - x}$ là:

A. $\frac{1 - 2 x}{x - 5}$

B. $\frac{- (2 x - 1)}{x - 5}$

C. $- \frac{1 - 2 x}{5 - x}$

D. $\frac{1 - 2 x}{5 - x}$

Xem đáp án

Đáp án D

Phương pháp:

Phân thức đối của phân thức $\frac{A}{B}$ là $- \frac{A}{B}$ .

Cách giải:

Phân thức đối của $\frac{2 x - 1}{5 - x}$ là $- \frac{2 x - 1}{5 - x} = \frac{1 - 2 x}{5 - x}$ .

Câu 2:

Giá trị của phân thức $\frac{x + 1}{2 x - 6}$ được xác định khi:

A. $x \neq 3$

B. $x \neq 1$

C. $x \neq - 3$

D. $x \neq - 1$

Xem đáp án

Đáp án A

Phương pháp:

Giá trị của phân thức $\frac{A}{B}$ xác định khi $B \neq 0$ .

Cách giải:

Giá trị của phân thức $\frac{x + 1}{2 x - 6}$ được xác định khi $2 x - 6 \neq 0 \Leftrightarrow 2 x \neq 6 \Leftrightarrow x \neq 3$ .

Câu 3:

Kết quả rút gọn của biểu thức $\frac{- 2 x^{2} - 2 x}{1 - x^{2}}$ là:

A. $\frac{- 2 x}{x + 1}$

B. $\frac{2 x}{x - 1}$

C. $\frac{2 x}{x + 1}$

D. $\frac{- 2 x}{x - 1}$

Xem đáp án

Đáp án B

Phương pháp:

Phân tích tử thức và mẫu thức thành nhân tử rồi rút gọn biểu thức.

Sử dụng hằng đẳng thức $a^{2} - b^{2} = (a - b) (a + b)$ .

Cách giải:

Ta có: $\frac{- 2 x^{2} - 2 x}{1 - x^{2}} = \frac{- 2 x (x + 1)}{(1 - x) (1 + x)}$

$= \frac{- 2 x}{1 - x} = \frac{2 x}{x - 1}$

Câu 4:

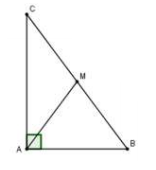
Cho $Δ A B C$ vuông tại $A$ có $A B = 3 c m$ , $A C = 4 c m$ . Độ dài đường trung tuyến $A M$ bằng:

A. $5 c m$

B. $2 c m$

C. $2,5 c m$

D. $10 c m$

Xem đáp án

Đáp án C

Phương pháp:

Sử dụng định lý Pytago để tính cạnh huyền

Sử dụng: Trong tam giác vuông, độ dài đường trung tuyến ứng với cạch huyền bằng nửa cạnh huyền.

Cách giải:

Xét tam giác $A B C$ vuông tại $A$ , theo định lý Pytago ta có: $B C = \sqrt{A B^{2} + A C^{2}} = \sqrt{3^{2} + 4^{2}} = 5 c m$

Vì $A M$ là đường trung tuyến ứng với cạnh huyền nên $A M = \frac{B C}{2} = \frac{5}{2} = 2,5 c m$ .

Câu 5:

Diện tích hình chữ nhật sẽ thay đổi như thế nào nếu chiều dài tăng 6 lần, chiều rộng giảm 2 lần?

A. Giảm 3 lần

B. Tăng 3 lần

C. Giảm 12 lần

D. Tăng 12 lần

Xem đáp án

Đáp án B

Phương pháp:

Diện tích hình chữ nhật có chiều dài $a$ , chiều rộng $b$ là $S = a b$ .

Cách giải:

Diện tích hình chữ nhật ban đầu là $S = a b$ với $a, b$ lần lượt là chiều dài và chiều rộng

Chiều dài mới là $a^{'} = 6 a$

Chiều rộng mới là $b^{'} = \frac{b}{2}$

Lúc này diện tích hình chữ nhật là $S^{'} = a^{'} . b^{'} = 6 a . \frac{b}{2} = 3 a b = 3 S$

Như vậy diện tích tăng 3 lần so với ban đầu.

Câu 6:

Chọn câu trả lời sai:

A. $\frac{4 x + 4}{4 x} = \frac{x + 1}{x}$

B. $\frac{x - 2}{x^{2} - 4} = \frac{1}{x + 2}$

C. $\frac{5 x + 5}{5 x} = 5$

D. $\frac{4 x^{2} - 9}{2 x + 3} = 2 x - 3$

Xem đáp án

Đáp án C

Phương pháp:

Phân tích tử thức và mẫu thức thành nhân tử rồi rút gọn biểu thức.

Cách giải:

Đáp án A: Ta có: $\frac{4 x + 4}{4 x} = \frac{4 (x + 1)}{4 x} = \frac{x + 1}{x}$ nên A đúng

Đáp án B: Ta có: $\frac{x - 2}{x^{2} - 4} = \frac{x - 2}{(x - 2) (x + 2)} = \frac{1}{x + 2}$ nên B đúng

Đáp án C: Ta có: $\frac{5 x + 5}{5 x} = \frac{5 (x + 1)}{5 x} = \frac{x + 1}{x} \neq 5$ nên C sai

Đáp án D: Ta có: $\frac{4 x^{2} - 9}{2 x + 3} = \frac{(2 x + 3) (2 x - 3)}{(2 x + 3)} = 2 x - 3$ nên D đúng

Câu 7:

Khẳng định nào sau đây đúng?

A. Hình bình hành có hai đường chéo vuông góc với nhau là hình chữ nhật.

B. Hình bình hành có hai cạnh kề bằng nhau là hình chữ nhật.

C. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

D.Hình bình hành có một đường chéo là tia phân giác của một góc là hình chữ nhật.

Xem đáp án

Đáp án C

Phương pháp:

Sử dụng dấu hiệu nhận biết hình chữ nhật.

Cách giải:

Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật nên C đúng.

Câu 8:

Phân thức $\frac{x + 2}{2 x}$ có giá trị bằng 1 khi $x$ bằng:

A.2

B.1

C.0

D. $\frac{3}{2}$

Xem đáp án

Đáp án A

Phương pháp:

Tìm điều kiện xác định.

Cho phân thức bằng 1 sau đó quy đồng mẫu thức để tìm $x$ .

So sánh điều kiện để kết luận

Cách giải:

ĐK: $2 x \neq 0 \Leftrightarrow x \neq 0$

Ta có:

$\frac{x + 2}{2 x} = 1 \Leftrightarrow \frac{x + 2}{2 x} = \frac{2 x}{2 x}$

$\Rightarrow x + 2 = 2 x$

$\Leftrightarrow x = 2$ (tm)

Vậy $x = 2$ .

Câu 9:

Tổng hai phân thức $\frac{x + 3}{2 x - 1}$ và $\frac{4 - x}{1 - 2 x}$ bằng phân thức nào sau đây:

A. $\frac{7}{2 x - 1}$

B.1

C.

\frac{7}{1 - 2 x}

D. $- 1$

Xem đáp án

Đáp án A

Phương pháp:

Đưa về cộng hai phân thức cùng mẫu: $\frac{A}{B} + \frac{C}{B} = \frac{A + C}{B}$ .

Cách giải:

Ta có:

$\frac{x + 3}{2 x - 1} + \frac{4 - x}{1 - 2 x} = \frac{x + 3}{2 x - 1} + \frac{4 - x}{2 x - 1}$

$= \frac{x + 3 + 4 - x}{2 x - 1} = \frac{7}{2 x - 1}$ .

Câu 10:

Khẳng định nào sau đây sai ?

A. Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình chữ nhật.

B.Hai tam giác bằng nhau thì có diện tích bằng nhau.

C. Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.

D. Hình thoi là hình có bốn trục đối xứng.

Xem đáp án

Đáp án D

Phương pháp:

Sử dụng kiến thức về hình chữ nhật, hai tam giác bằng nhau, trục đối xứng.

Cách giải:

Ta có A, B, C đều đúng.

D sai vì hình thoi có hai trục đối xứng là hai đường chéo.

Câu 11:

Thực hiện phép chia $x^{3} + 27$ cho $3 x - 9 - x^{2}$ ta được thương là:

A. $x + 3$

B. $x - 3$

C. $- x - 3$

D. $- x + 3$

Xem đáp án

Đáp án C

Phương pháp:

Sử dụng hằng đẳng thức $a^{3} + b^{3} = (a + b) (a^{2} - a b + b^{2})$

Cách giải:

Ta có:

$(x^{3} + 27) : (3 x - 9 - x^{2})$

$= (x + 3) : (x^{2} - 3 x + 9) : [- (x^{2} - 3 x + 9)]$

$= - (x + 3) = - x - 3$

Câu 12:

Hình vuông có đường chéo bằng 4 thì cạnh của nó bằng:

A.2

B.8

C.4

D. $\sqrt{8}$

Xem đáp án

Đáp án D

Phương pháp:

Hình vuông có bốn cạnh bằng nhau.

Sử dụng định lý Pytago.

Cách giải:

Xét hình vuông $A B C D$ có đường chéo .

Áp dụng định lý Pytago cho tam giác vuông $A B C$ ta có:

$A B^{2} + B C^{2} = A C^{2}$

$\Leftrightarrow 2 A B^{2} = 4^{2}$

$\Leftrightarrow A B^{2} = 8$

$\Rightarrow A B = \sqrt{8}$

Vậy hình vuông có cạnh là $\sqrt{8}$ .

Câu 13:

Cho biểu thức

A = (\frac{3 x}{x - 2} - \frac{2 x^{2} - 5}{x^{2} - 4} - \frac{x - 1}{x + 2}) : \frac{3}{x + 2}

Rút gọn và tìm điều kiện xác định của .

Xem đáp án

Phương pháp:

Quy đồng mẫu và rút gọn.

Cách giải:

Rút gọn và tìm điều kiện xác định của $A$ .

$A = (\frac{3 x}{x - 2} - \frac{2 x^{2} - 5}{x^{2} - 4} - \frac{x - 1}{x + 2}) : \frac{3}{x + 2}$

DK: $\{\begin{cases} x - 2 \neq 0 \\ x + 2 \neq 0 \Leftrightarrow x \neq \pm 2 \\ x^{2} - 4 \neq 0 \end{cases}$

$A = (\frac{3 x (x + 2)}{(x - 2) (x + 2)} - \frac{2 x^{2} - 5}{(x - 2) (x + 2)} - \frac{(x - 1) (x - 2)}{(x - 2) (x + 2)}) : \frac{3}{x + 2}$

$A = (\frac{3 x^{2} + 6 x - 2 x^{2} + 5 - x^{2} + x + 2 x - 2}{(x - 2) (x + 2)}) : \frac{3}{x + 2}$

$A = \frac{9 x + 3}{(x - 2) (x + 2)} . \frac{x + 2}{3}$

$A = \frac{3 (3 x + 1)}{(x - 2) (x + 2)} . \frac{x + 2}{3}$

$A = \frac{3 x + 1}{x - 2}$

Câu 14:

Cho biểu thức

A = (\frac{3 x}{x - 2} - \frac{2 x^{2} - 5}{x^{2} - 4} - \frac{x - 1}{x + 2}) : \frac{3}{x + 2}

Tính giá trị của x biết

x^{2} - 2 x = 0

.

Xem đáp án

Phương pháp

Tìm $x$ rồi thay vào $A$ .

Cách giải:

Tính giá trị của biết .

Ta có:

$x^{2} - 2 x = 0 \Leftrightarrow x (x - 2) = 0$ .

$\Leftrightarrow [\begin{array}{l} x = 0 \\ x - 2 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 0 (t m) \\ x = 2 (k t m) \end{array}$

Thay $x = 0$ vào $A$ ta được: $A = \frac{3.0 + 1}{0 - 2} = - \frac{1}{2}$ .

Vậy với $x = 0$ thì $A = - \frac{1}{2}$ .

Câu 15:

Cho biểu thức

A = (\frac{3 x}{x - 2} - \frac{2 x^{2} - 5}{x^{2} - 4} - \frac{x - 1}{x + 2}) : \frac{3}{x + 2}

Tìm các giá trị nguyên của để có giá trị nguyên.

Xem đáp án

Tìm các giá trị nguyên của để có giá trị nguyên.

Ta có: $A = \frac{3 x + 1}{x - 2} = \frac{3 x - 6 + 7}{x - 2} = \frac{3 x - 6}{x - 2} + \frac{7}{x - 2} = 3 + \frac{7}{x - 2}$

Vì $x \in ℤ$ và $3 \in ℤ$ nên để $A \in ℤ$ thì $x - 2 \in U (7) = \{\pm 1; \pm 7\}$ .

Ta có bảng:

$x - 2$	1	$- 1$	7
$x$	3 (tm)	1 (tm)	9 (tm)	(tm)

Vậy với $x \in \{3; 1; 9; - 5\}$ thì $A \in ℤ$ .

Câu 16:

Tìm

x

, biết:

4 x^{2} - 1 - (1 - 2 x) (x + 2) = 0

Xem đáp án

Phương pháp:

Đưa phương trình về dạng tích.

Tìm $x$ , biết:

4 x^{2} - 1 - (1 - 2 x) (x + 2) = 0

\Leftrightarrow (2 x - 1) (2 x + 1) + (2 x - 1) (x + 2) = 0

\Leftrightarrow (2 x - 1) (2 x + 1 + x + 2) = 0

\Leftrightarrow (2 x - 1) (3 x + 3) = 0

.

\Leftrightarrow [\begin{array}{l} 2 x - 1 = 0 \\ 3 x + 3 = 0 \end{array} \Leftrightarrow [\begin{array}{l} 2 x = 1 \\ 3 x = - 3 \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{1}{2} \\ x = - 1 \end{array}

Vậy phương trình có tập nghiệm $S = \{\frac{1}{2}; - 1\}$ .

Câu 17:

Tìm x, biết:

\frac{3 x - x^{2}}{x^{2} - 9} = 0

Xem đáp án

Phương pháp:

Đặt điều kiện xác định và giải phương trình.

Cách giải:

\frac{3 x - x^{2}}{x^{2} - 9} = 0

.

ĐK: $x^{2} - 9 \neq 0 \Leftrightarrow x^{2} \neq 9 \Leftrightarrow x \neq \pm 3$

Khi đó

$3 x - x^{2} = 0 \Leftrightarrow x (3 - x) = 0$

$\Leftrightarrow [\begin{array}{l} x = 0 \\ 3 - x = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 0 (t m) \\ x = 3 (k t m) \end{array}$ .

Vậy phương trình có nghiệm $x = 0$ .

Câu 18:

Tìm , biết:

Tìm

a

và

b

để

f (x) = x^{4} - 3 x^{3} + 3 x^{2} + a x + b

chia hết cho

g (x) = x^{2} - 3 x + 4

.

Xem đáp án

Tìm $a$ và $b$ để $f (x) = x^{4} - 3 x^{3} + 3 x^{2} + a x + b$ chia hết cho $g (x) = x^{2} - 3 x + 4$ .

Ta có:

$f (x) = x^{4} - 3 x^{3} + 3 x^{2} + a x + b$

$= (x^{4} - 3 x^{3} + 4 x^{2}) - (x^{2} - 3 x + 4) + a x - 3 x + b + 4$

$= (x^{2} - 3 x + 4) (x^{2} - 1) + (a - 3) x + b + 4$

$= x^{2} (x^{2} - 3 x + 4) - (x^{2} - 3 x + 4) + (a - 3) x + b + 4$

$= (x^{2} - 1) f (x) + (a - 3) x + b + 4$

Để $f (x)$ chia hết cho $g (x)$ thì $\{\begin{cases} a - 3 = 0 \\ b + 4 = 0 \end{cases} \Leftrightarrow \{\begin{cases} a = 3 \\ b = - 4 \end{cases}$ .

Vậy $a = 3$ , $b = - 4$ .

Câu 19:

Cho

Δ A B C

vuông tại

A

. Gọi

D

là trung điểm của

B C

, kẻ

D E

vuông góc với

A B

tại

E

. Gọi

I

là điểm đối xứng với

D

qua

A C, D I

cắt

A C

tại

F

.

Chứng minh tứ giác

A E D F

là hình chữ nhật.

Xem đáp án

Phương pháp:

Chứng minh tứ giác có ba góc vuông là hình chữ nhật.

Cách giải:

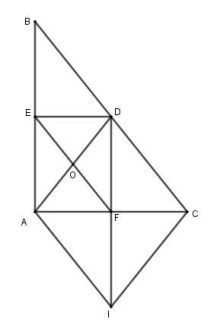
Chứng minh tứ giác $A E D F$ là hình chữ nhật.

Ta có: $D E ⊥ A B \Leftrightarrow E = 90 °$

$D F ⊥ A C \Leftrightarrow F = 90 °$

Tứ giác $A E D F$ có $A = E = F = 90 °$ nên $A E D F$ là hình chữ nhật (đpcm).

Câu 20:

Cho

Δ A B C

vuông tại

A

. Gọi

D

là trung điểm của

B C

, kẻ

D E

vuông góc với

A B

tại

E

. Gọi

I

là điểm đối xứng với

D

qua

A C, D I

cắt

A C

tại

F

.

Gọi

O

là giao điểm của

A D

và

E F

. Chứng minh tứ giác

A B D I

là hình bình hành và từ đó suy ra ba điểm

B, O, I

thẳng hàng.

Xem đáp án

Phương pháp:

Chứng minh tứ giác có một cặp cạnh đối vừa song song vừa bằng nhau là hình bình hành.

Cách giải:

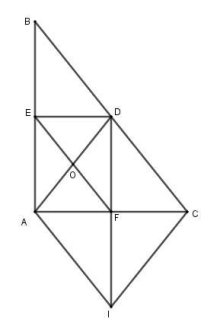
Gọi $O$ là giao điểm của $A D$ và $E F$ . Chứng minh tứ giác $A B D I$ là hình bình hành và từ đó suy ra ba điểm $B, O, I$ thẳng hàng.

Ta có: $\{\begin{cases} D F ⊥ A C \\ A B ⊥ A C \end{cases}$ nên $D F / / A B$ (từ vuông góc đến song song)

Mà $D$ là trung điểm $B C$ nên $F$ là trung điểm $A C$

$\Rightarrow D F$ là đường trung bình của tam giác $A C B \Rightarrow D F = \frac{1}{2} A B (t / c) \Rightarrow A B = 2 D F$

Mà $D I = 2 D F$ (do $I$ đối xứng với $D$ qua $A C$ )

Do đó $D I = A B (= 2 D F)$ .

Mà $D I / / A B$ nên tứ giác $A B D I$ là hình bình hành (dhnb).

Vì $O$ là giao điểm của $E F$ với $A D$ nên $O$ là trung điểm $A D$ .

Tứ giác $A B D I$ là hình bình hành $\Rightarrow$ hai đường chéo $B I, A D$ cắt nhau tại $O$ là trung điểm của mỗi đường.

Vậy $B, O, I$ thẳng hàng.

Câu 21:

Cho

Δ A B C

vuông tại

A

. Gọi

D

là trung điểm của

B C

, kẻ

D E

vuông góc với

A B

tại

E

. Gọi

I

là điểm đối xứng với

D

qua

A C, D I

cắt

A C

tại

F

.

Tam giác

A B C

cần thêm điều kiện gì để tứ giác

A B C I

là hình thang cân. Hãy tính trong trường hợp này biết

A D = 8 c m

.

Xem đáp án

Phương pháp:

Sử dụng hình thang có hai góc kề một đáy bằng nhau là hình thang cân.

Cách giải:

Tam giác $A B C$ cần thêm điều kiện gì để tứ giác $A B C I$ là hình thang cân. Hãy tính trong trường hợp này biết .

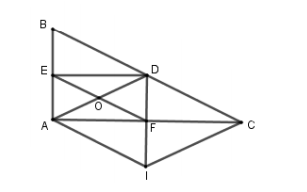
Ta có: $A I / / B C$ (do $A I / / B D$ ) nên tứ giác $A I C B$ là hình thang.

Để $A I C B$ là hình thang cân thì $A B C = I C B$

Xét tứ giác $A I C D$ có $A C$ vuông góc $D I$ tại trung điểm mỗi đường nên là hình thoi.

$\Rightarrow C A$ là tia phân giác góc .

$\Rightarrow I C B = 2 A C B$

Từ đó $A B C = 2 A C B$ .

Mà $A B C + A C B = 90 ° \Leftrightarrow A C B = 30 °$ .

Vậy tam giác $A B C$ cần thêm điều kiện $A C B = 30 °$ để tứ giác $A I C B$ là hình thang cân.

Tam giác $A B C$ vuông tại $A$ có $A C B = 30 °$ nên $A B = \frac{1}{2} B C$ .

Mà $B C = 2 A D = 2.8 = 16$ nên $A B = \frac{1}{2} .16 = 8$ .

Áp dụng định lí Pi-ta-go ta có: $A B^{2} + A C^{2} = B C^{2} \Leftrightarrow 8^{2} + A C^{2} = 16^{2} \Leftrightarrow A C^{2} = 16^{2} - 8^{2} = 192 \Rightarrow A C = 8 \sqrt{3}$

Diện tích tam giác: $S_{A B C} = \frac{1}{2} A B . A C = \frac{1}{2} .8.8 \sqrt{3} = 32 \sqrt{3}$ .

Câu 22:

Cho

x, y \in ℝ

và

x \neq y

. Tìm giá trị nhỏ nhất của biểu thức

P = \frac{x^{2} - 6 x y + 6 y^{2}}{x^{2} - 2 x y + y^{2}}

.

Xem đáp án

Phương pháp:

Xét $y = 0$

Xét $y \neq 0$ , chia cả tử và mẫu cho $y^{2}$ . Sau đó ta chứng minh biểu thức thu được lớn hơn hoặc bằng $- 3$ .

Cách giải:

Xét $y = 0$ , ta có: $P = 1$ .

Xét $y \neq 0$ , chia cả tử và mẫu của $(1)$ cho $y^{2}$ , ta có:

$P = \frac{{(\frac{x}{y})}^{2} - 6 (\frac{x}{y}) + 6}{{(\frac{x}{y})}^{2} - 2 (\frac{x}{y}) + 1}$

Đặt $t = \frac{x}{y} (t \neq 1)$ . Biểu thức $P$ trở thành:

$P = \frac{t^{2} - 6 t + 6}{t^{2} - 2 t + 1}$

Ta sẽ đi chứng minh: $P \geq - 3 (*)$

Ta có:

$\frac{t^{2} - 6 t + 6}{t^{2} - 2 t + 1} \geq - 3$

$\Leftrightarrow t^{2} - 6 t + 6 \geq - 3 t^{2} + 6 t - 3$

$\Leftrightarrow 4 t^{2} - 12 t + 9 \geq 0$

$\Leftrightarrow {(2 t - 3)}^{2} \geq 0$

$\Rightarrow (*)$ luôn đúng.

Dấu $" = "$ xảy ra $\Leftrightarrow 2 t - 3 = 0 \Leftrightarrow t = \frac{3}{2} \Leftrightarrow \frac{x}{y} = \frac{3}{2} \Leftrightarrow 2 x = 3 y$ .

Vậy $\min P = - 3$ , đạt được khi $2 x = 3 y$ .