13 câu hỏi trắc nghiệm thuộc Bộ 14 đề thi Học kì 1 Toán 8 có đáp án - Đề 12

Câu 1:

Phân tích các đa thức sau thành nhân tử: $5 x - 20 x y$

Xem đáp án

Phương pháp:

Sử dụng các phương pháp cơ bản như đặt nhân tử chung, nhóm hạng tử, hằng đẳng thức…

Cách giải: $5 x - 20 x y = 5 x (1 - 4 y)$

Câu 2:

Phân tích các đa thức sau thành nhân tử: $x^{3} - 4 x y^{2}$

Xem đáp án

Phương pháp:

Sử dụng các phương pháp cơ bản như đặt nhân tử chung, nhóm hạng tử, hằng đẳng thức…

Cách giải:

$x^{3} - 4 x y^{2} = x (x^{2} - 4 y^{2}) = x (x - 2 y) (x + 2 y)$

Câu 3:

Phân tích các đa thức sau thành nhân tử: $3 x^{2} - 3 x y - 5 x + 5 y$

Xem đáp án

Phương pháp:

Sử dụng các phương pháp cơ bản như đặt nhân tử chung, nhóm hạng tử, hằng đẳng thức…

Cách giải:

$3 x^{2} - 3 x y - 5 x + 5 y = 3 x (x - y) - 5 (x - y) = (3 x - 5) (x - y)$

Câu 4:

Tìm x biết: $2 (x + 7) - 2 = 18$

Xem đáp án

Phương pháp:

Sử dụng biến đổi cơ bản và phân tích đa thức thành nhân tử.

Cách giải:

$2 (x + 7) - 2 = 18$

$\Leftrightarrow 2 x + 14 - 2 = 18$

$\Leftrightarrow 2 x = 6$

$\Leftrightarrow x = 3$

Vậy $x = 3$

Câu 5:

Tìm x biết: $2 x (x - 5) = 4 (x - 5)$

Xem đáp án

Phương pháp:

Sử dụng biến đổi cơ bản và phân tích đa thức thành nhân tử.

Cách giải:

$2 x (x - 5) = 4 (x - 5)$

$\Leftrightarrow 2 x (x - 5) - 4 (x - 5) = 0$

$\Leftrightarrow (2 x - 4) (x - 5) = 0$

$\Leftrightarrow [\begin{array}{l} 2 x - 4 = 0 \\ x - 5 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 2 \\ x = 5 \end{array}$

Vậy

x = 2

hoặc

x = 5

.

Câu 6:

Thực hiện các phép tính sau: $(x - 3) (2 x + 5)$

Xem đáp án

Phương pháp:

Nhân và chia đa thức, đặt nhân tử chung.

Cách giải:

$(x - 3) (2 x + 5) = 2 x^{2} + 5 x - 6 x - 15 = 2 x^{2} - x - 15$

Câu 7:

Thực hiện các phép tính sau: $(9 x^{2} y^{3} + 18 x^{2} y^{2} - 3 x y^{2}) : 9 x y^{2}$

Xem đáp án

Phương pháp:

Nhân và chia đa thức, đặt nhân tử chung.

Cách giải:

$(9 x^{2} y^{3} + 18 x^{2} y^{2} - 3 x y^{2}) : 9 x y^{2}$

$= 3 x y^{2} (3 x y + 6 x - 1) : 9 x y^{2}$

$= \frac{3 x y + 6 x - 1}{3}$

Câu 8:

Rút gọn biểu thức $M = (x + 1) (x^{2} - x + 1) - (x^{3} - 9)$ .

Xem đáp án

Phương pháp:Sử dụng hằng đẳng thức.

Cách giải:

$M = (x + 1) (x^{2} - x + 1) - (x^{3} - 9)$

$M = (x^{3} + 1) - (x^{3} - 9)$

$M = 10$

Câu 9:

Tìm số thực a để đa thức

x^{3} + 2 x^{2} + a

chia hết cho đa thức

x + 3

.

Xem đáp án

Phương pháp:Phân tích đa thức, dùng tính chất của phép chia hết (có dư bằng 0).

Cách giải:

Ta có:

$\Rightarrow x^{3} + 2 x^{2} + a = (x + 3) (x^{2} - x + 3) - 9 + a$

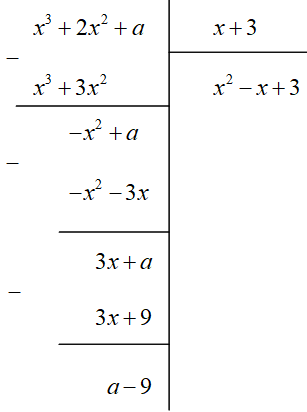
Để đa thức $x^{3} + 2 x^{2} + a$ chia hết cho đa thức $x + 3$ thì $- 9 + a = 0 \Leftrightarrow a = 9$ .

Vậy $a = 9$ .

Câu 10:

Cho hình vuông ABCD, M là trung điểm của AB. Gọi P là điểm đối xứng với M qua B, N là điểm đối xứng với C qua B.

Chứng minh tứ giác MNPC là hình thoi.

Xem đáp án

Phương pháp:

Sử dụng dấu hiệu nhân biết hình thoi, hình bình hành.

Cách giải:

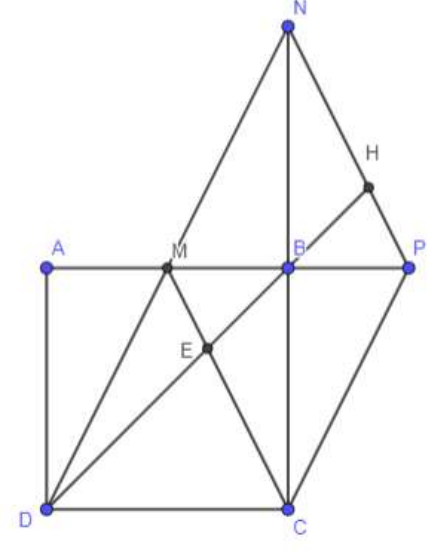
Vì P là điểm đối xứng với M qua B, N là điểm đối xứng với C qua B nên MNPC là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường).

Lại có $∠ A B C = 90 °$ $\Rightarrow A B ⊥ B C$

hay $M P ⊥ N C \Rightarrow M N P C$ là hình thoi.(dhnb)

Câu 11:

Cho hình vuông ABCD, M là trung điểm của AB. Gọi P là điểm đối xứng với M qua B, N là điểm đối xứng với C qua B.

Chứng minh N đối xứng với D qua M.

Xem đáp án

Phương pháp:

Chứng minh bằng nhau và thẳng hàng.

Cách giải:

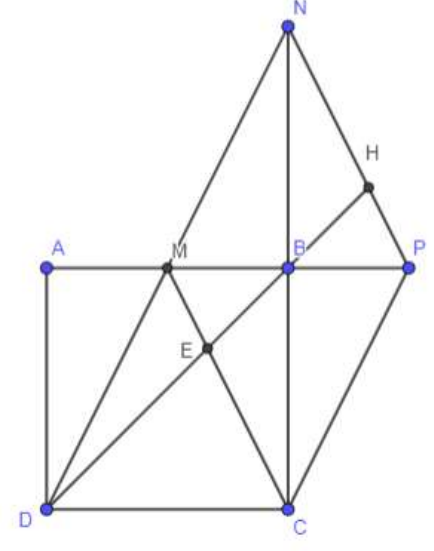
Vì M là trung điểm của AB nên AM = MB.

Xét $Δ A M D$ và $Δ B M C$ ta có:

$∠ D A M = ∠ C B M = 90 °$

$A M = B M$ (cmt)

$A D = B C$ (gt)

$\Rightarrow Δ A M D = Δ B M C$ (2cgv) $\Rightarrow M D = M C$ .

Mà $M C = M N$ (MNPC là hình thoi)

Suy ra $M D = M N$ . (1)

Tứ giác MPCD có $M P = D C, M P / / D C$ suy ra MPCD là hình bình hành, suy ra $M D / / P C$ .

Lại có $P C / / M N \Rightarrow D, M, N$ thẳng hàng. (2)

Từ (1) và (2) suy ra N đối xứng với D qua M.

Câu 12:

Cho hình vuông ABCD, M là trung điểm của AB. Gọi P là điểm đối xứng với M qua B, N là điểm đối xứng với C qua B.

Gọi H là giao điểm của DB và NP. Tính tỉ số $\frac{N P}{H P}$

Xem đáp án

Phương pháp:

Bắc cầu tỉ số, sử dụng định lý Thales.

Cách giải:

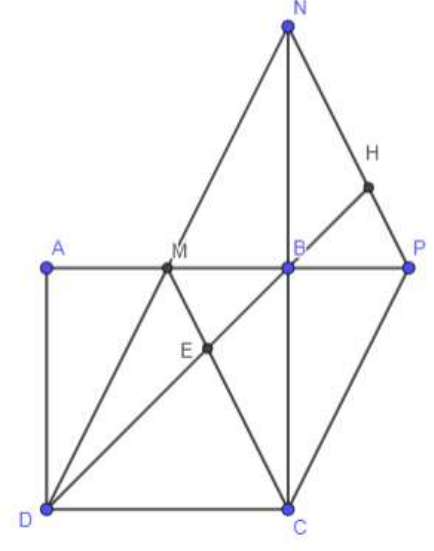
Gọi E là giao điểm của DB và CM.

Xét $Δ B E M$ và $Δ B H P$ ta có:

$∠ B M E = ∠ B P H$ (so le trong)

$B M = B P$ (MNPC là hình thoi)

$∠ N B E = ∠ H B P$ (hai góc đối đỉnh)

$\Rightarrow Δ B E M = Δ B H P$ (g – c – g).

$\Rightarrow H P = E M$ (hai cạnh tương ứng).

Lại có: $N P = C M \Rightarrow \frac{N P}{H P} = \frac{C M}{E M}$ .

Theo định lý Ta-lét:

$\frac{C E}{E M} = \frac{D C}{M B} = 2 \Rightarrow \frac{C E + E M}{E M} = 3 \Rightarrow \frac{C M}{E M} = 3$

Suy ra

\frac{N P}{H P} = 3

.

Câu 13:

Cho các số thực a, b, c thỏa mãn: $(a + b + c) (a b + b c + c a) = 2018$ và $a b c = 2018$ .

Tính giá trị của biểu thức $P = (b^{2} c + 2018) (c^{2} a + 2018) (a^{2} b + 2018)$ .

Xem đáp án

Phương pháp:

Từ điều kiện đề bài, phân tích và đưa về bài toán cơ bản.

Cách giải:

$(a + b + c) (a b + b c + c a) = 2018$ và $a b c = 2018$ suy ra $a + b + c \neq 0$ , $a b c \neq 0$

và $(a + b + c) (a b + b c + c a) = a b c (= 2018)$

$\Rightarrow (a + b + c) \frac{(a b + b c + c a)}{a b c} = 1$

$\Rightarrow (a + b + c) (\frac{1}{a} + \frac{1}{b} + \frac{1}{c}) = 1 \Rightarrow \frac{1}{a} + \frac{1}{b} + \frac{1}{c} = \frac{1}{a + b + c}$

$\Rightarrow (\frac{1}{a} + \frac{1}{b}) + \frac{1}{c} - \frac{1}{a + b + c} = 0$

$\Rightarrow \frac{a + b}{a b} + \frac{a + b + c - c}{c (a + b + c)} = 0$

$\Rightarrow \frac{a + b}{a b} + \frac{a + b}{c (a + b + c)} = 0$

$\Rightarrow (a + b) (\frac{1}{a b} + \frac{1}{c (a + b + c)}) = 0$

$\Rightarrow (a + b) [\frac{(c + a) (c + b)}{a b c (a + b + c)}] = 0$

$\Rightarrow (a + b) (c + a) (c + b) = 0 \Leftrightarrow [\begin{array}{l} a = - b \\ b = - c \\ c = - a \end{array}$

Không mất tính tổng quát giả sử $a = - b$ , từ điều kiện ta có $a b c = 2018$

$\Rightarrow - b . b . c = 2018$ $\Rightarrow b^{2} c + 2018 = 0 \Rightarrow P = 0$

Vậy $P = 0$ .