Chiếc cầu dây văng một nhịp được thiết kế hai bên thành cầu có dạng parabol và được cố định bằng các dây cáp song song.
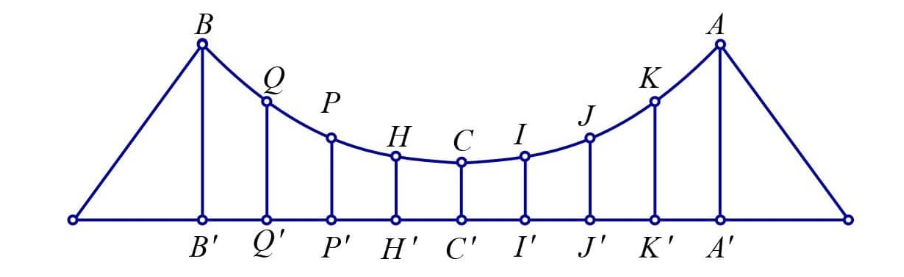
Dựa vào bản vẽ ở Hình 14, hãy tính chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên. Biết:
– Dây dài nhất là 5m, dây ngắn nhất là 0,8 m. Khoảng cách giữa các dây bằng nhau.
– Nhịp cầu dài 30 m.
– Cần tính thêm 5% chiều dài mỗi sợi dây cáp để neo cố định.

 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
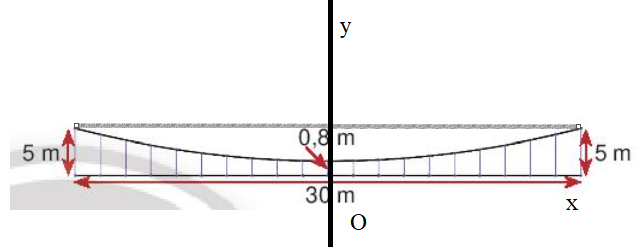
Chọn hệ trục tọa độ như hình vẽ.
Trong đó, khoảng cách giữa các dây bằng nhau và có 20 khoảng cách nên mỗi khoảng cách ứng với 1,5 m.
Gọi dạng parabol của thành cầu là đồ thị của hàm số y = ax2 + bx + c (a ≠ 0).
Đồ thị hàm số cắt trục tung tại điểm (0; 0,8) nên ta có:
a.02 + b.0 + c = 0,8 ⇒ c = 0,8
Tại hai đầu cầu, tức y = 5 thì ta có hai giá trị x thỏa mãn là x1 = –15 và x2 = 15
Từ đó ta có:
a.(–15)2 + b.(–15) + 0,8 = 5 ⇒ 225a – 15b = 4,2 (1)
a.152 + b.15 + 0,8 = 5 ⇒ 225a + 15b = 4,2 (2)
Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}225a - 15b = 4,2\\225a + 15b = 4,2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{7}{{375}}\\b = 0\end{array} \right.\)
Vậy phương trình parabol cần tìm là: \(y = \frac{7}{{375}}{x^2} + 0,8\)
Độ dài mỗi dây ở vị trí hoành độ tương ứng là:
Tại x = 0, độ dài dây là: 0,8 + 5%.0,8 = 0,84 (m)
Tại x = 1,5 và x = –1,5 thì độ dài dây là:
\(\frac{7}{{375}}{.1,5^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.1,5}^2} + 0,8} \right) = 0,8841\) (m)
Tại x = 3 và x = –3 thì độ dài dây là:
\(\frac{7}{{375}}{.3^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.3}^2} + 0,8} \right) = 1,0164\) (m)
Tại x = 4,5 và x = –4,5 thì độ dài dây là:
\(\frac{7}{{375}}{.4,5^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.4,5}^2} + 0,8} \right) = 1,2369\) (m)
Tại x = 6 và x = –6 thì độ dài dây là:
\(\frac{7}{{375}}{.6^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.6}^2} + 0,8} \right) = 1,5456\) (m)
Tại x = 7,5 và x = –7,5 thì độ dài dây là:
\(\frac{7}{{375}}{.7,5^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.7,5}^2} + 0,8} \right) = 1,9425\) (m)
Tại x = 9 và x = –9 thì độ dài dây là:
\(\frac{7}{{375}}{.9^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.9}^2} + 0,8} \right) = 2,4276\) (m)
Tại x = 10,5 và x = –10,5 thì độ dài dây là:
\(\frac{7}{{375}}{.10,5^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.10,5}^2} + 0,8} \right) = 3,0009\)(m)
Tại x = 12 và x = –12 thì độ dài dây là:
\(\frac{7}{{375}}{.12^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.12}^2} + 0,8} \right) = 3,6624\)(m)
Tại x = 13,5 và x = –13,5 thì độ dài dây là:
\(\frac{7}{{375}}{.13,5^2} + 0,8 + 5\% .\left( {\frac{7}{{375}}{{.13,5}^2} + 0,8} \right) = 4,4121\)(m)
Tại x = 15 và x = –15 thì độ dài dây là:
5 + 5%.5 = 5,25 (m)
Chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên của cầu là:
2.0,84 + 4 . (0,8841 + 1,0164 + 1,2369 + 1,5456 + 1,9425 + 2,4276 + 3,0009 + 3,6624 + 4,4121 + 5,25) = 103,194 (m).

Giả sử một máy bay cứu trợ đang bay theo phương ngang và bắt đầu thả hàng từ độ cao 80 m, lúc đó máy bay đang bay với vận tốc 50 m/s. Để thùng hàng cứu trợ rơi đúng vị trí được chọn, máy bay cần bắt đầu thả hàng từ vị trí cách vị trí được chọn bao nhiêu mét ? Biết rằng nếu chọn gốc tọa độ là hình chiếu trên mặt đất của vị trí hàng cứu trợ bắt đầu được thả, thì tọa độ của hàng cứu trợ được cho bởi hệ sau: \(\left\{ \begin{array}{l}x = {v_o}t\\y = h - \frac{1}{2}g{t^2}\end{array} \right.\)
trong đó, v0 là vận tốc ban đầu và h là độ cao tính từ khi hàng rời máy bay.
Lưu ý: Chuyển động này được xem là chuyển động ném ngang.