A. \(\frac{{{S_{AMN}}}}{{{S_{ABC}}}} = \frac{{AM}}{{AB}}.\frac{{AN}}{{AC}}\);
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: A.
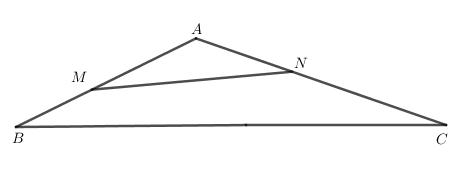
Diện tích tam giác AMN là: \({S_{AMN}} = \frac{1}{2}.AM.AN.\sin \widehat {MAN}\).
Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}.AB.AC.\sin \widehat {BAC}\).
Do \(\widehat {MAN} = \widehat {BAC}\) (hai góc trùng nhau)
Nên \(\frac{{{S_{AMN}}}}{{{S_{ABC}}}} = \frac{{AM}}{{AB}}.\frac{{AN}}{{AC}}\).
Tam giác ABC có BC = a, CA = b, AB = c.
Chứng minh rằng: a = b.cos C + c.cos B.
Cho tam giác ABC có BC = a, AC = b, AB = c. Khẳng định nào sau đây là đúng?