 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: D.
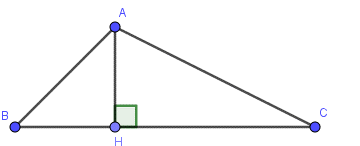
Áp dụng định lý Pythagore ta có:
BH = \(\sqrt {A{B^2} - A{H^2}} = \sqrt {{{\left( {2\sqrt 2 } \right)}^2} - {2^2}} = 2\)
Tương tự: CH = \(\sqrt {A{C^2} - A{H^2}} = \sqrt {{{\left( {2\sqrt 3 } \right)}^2} - {2^2}} = 2\sqrt 2 \).
Do đó BC = BH + CH = 2 + 2\(\sqrt 2 \).
Vậy diện tích tam giác ABC là: S = \(\frac{1}{2}\)AH.BC = \(\frac{1}{2}\). 2. (2 + 2\(\sqrt 2 \)) = 2 + 2\(\sqrt 2 \).
Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu cạnh AB tăng lên 3 lần, cạnh AC tăng lên 4 lần và giữ nguyên độ lớn của góc A thì khi đó diện tích của tam giác mới được tạo nên bằng: