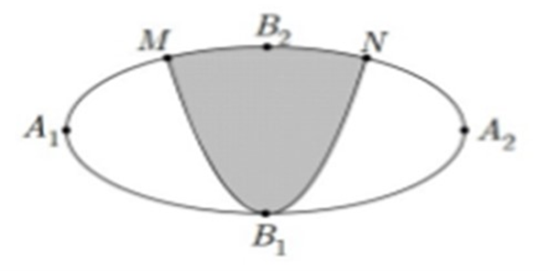
Một biển quảng cáo có dạng hình Elip với bốn đỉnh A1, A2, B1, B2 như hình vẽ bên. Người ta chia elip bởi parabol có đỉnh B1, trục đối xứng B1B2 và đi qua các điểm M, N. Sau đó sơn phần tô đậm với giá 100 000 đồng/m2 và trang trí đèn Led cho phần còn lại với giá 300 000 đồng/m2. Tính số tiền để hoàn thành biển quảng cáo trên (làm tròn đến hàng nghìn), biết A1A2 = 6m, B1B2 = 4m, MN = 4m.
A. 2 456 000 đồng;
B. 2 015 000 đồng;
C. 3 072 000 đồng;
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
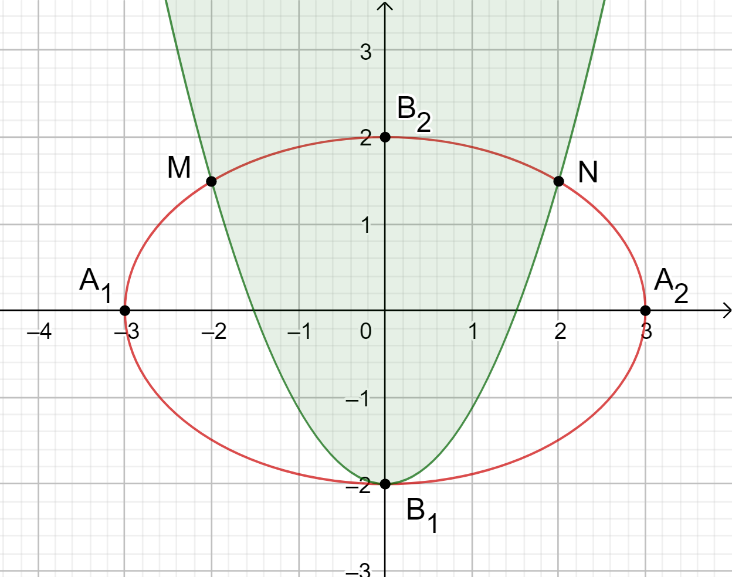
Gán hình dạng của biển quảng cáo vào hệ trục tọa độ Oxy như hình vẽ.
Gọi S là diện tích của hình elip, S1 là diện tích phần tô đậm và S2 là diện tích phần còn lại.
Hình elip có A1A2 = 6 m, B1B2 = 4 m nên suy ra a = 3 m, b = 4 m.
Phương tình elip là:
Diện tích hình elip là S = pab = 6p.
Thay hoành độ của M, N vào phương tình elip ta suy ra được tọa độ hai điểmPhương trình parabol có đỉnh B1, trục đối xứng B1B2 và đi qua các điểm M, N có dạng: y = ax2 - 2.
Điểm M thuộc parabol nên suy ra
Vậy suy ra
Diện tích phần tô đậm là:
» 10,7055
Þ S2 = S - S1 = 6p - S1
Số tiền để hoàn thành biển quảng cáo trên là
100 000S1 + 300 000S2 = 100 000S1 + 300 000(6p - S1)
= 3 600 000p - 200 000S1
» 1 800 000p - 200 000.10,7055
» 3 513 766 (đồng).
Cho hàm số f (x) có đạo hàm liên tục trên ℝ, f (0) = 0, f '(0) ¹ 0 và thỏa mãn hệ thức f (x).f '(x) + 18x2 = (3x2 + x).f '(x) + (6x + 1).f (x), "x Î ℝ.
Biết , với a, b, c là các số nguyên. Tính giá trị biểu thức P = 2a + 3b + c.
Gọi z1, z2 là hai nghiệm phức của phương trình z2 + 2z + 10 = 0. Giá trị của biểu thức |z1| + |z2| bằng
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có A(-1; 1; 6), B(-3; -2; -4), C(1; 2; -1), D(2; -2; 0). Tìm tọa độ điểm M thuộc đường thẳng CD sao cho tam giác ABM có chu vi nhỏ nhất.
Diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số y = f (x), y = g (x) liên tục trên [a; b] và hai đường thẳng x = a, x = b (a < b) được tính theo công thức
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và mặt phẳng (P): x - y - z + 3 = 0. Đường thẳng D đi qua M(1; 1; 2) song song với mặt phẳng (P) và vuông góc với đường thẳng d có phương trình là
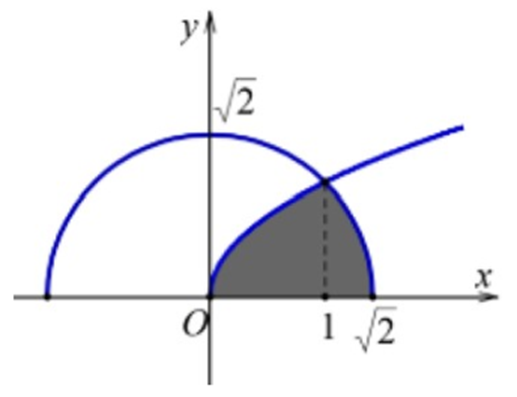
Cho (H) là hình phẳng giới hạn bởi đường cong có phương trình , nửa đường tròn với và trục hoành (phần tô đậm trong hình vẽ). Diện tích của hình (H) bằng
Cho số phức z thỏa mãn . Biết tập hợp các điểm biểu diễn số phức w = (2 - i)z - 3i + 5 là một đường tròn. Xác định tâm I và bán kính R của đường tròn đó.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-1; 0; 3), B(3; 6; -7). Tọa độ trung điểm I của đoạn thẳng AB là