Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
Biểu diễn miền nghiệm của hệ bất phương trình trên mặt phẳng Oxy:
• Miền nghiệm của bất phương trình x – y – 1 ≤ 0 là nửa mặt phẳng (kể cả bờ d1: x – y – 1 = 0) chứa điểm O(0; 0).
• Miền nghiệm của bất phương trình x + 4y + 9 ≥ 0 là nửa mặt phẳng (kể cả bờ d2: x + 4y + 9 = 0) chứa điểm O(0; 0).
• Miền nghiệm của bất phương trình x – 2y + 3 ≥ 0 là nửa mặt phẳng (kể cả bờ d1: x – y – 1 = 0) chứa điểm O(0; 0).
Miền không gạch chéo (kể cả bờ d1, d2) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.
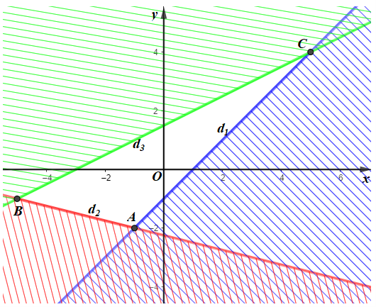
Miền nghiệm của hệ bất phương trình là miền tam giác ABC với A(–1; –2), B(–5; –1) và C(5; 4).
Xét biểu thức F(x; y) = 3x – 2y – 4.
Tại A(–1; –2): F = 3.(–1) – 2.(–2) – 4 = –3.
Tại B(–5; –1): F = 3.(–5) – 2.(–1) – 4 = –17.
Tại C(5; 4): F = 3.5 – 2.4 – 4 = 3.
F(x; y) đạt giá trị nhỏ nhất bằng –17 tại B(–5; –1).
Vậy ta chọn phương án B.Cho hệ bất phương trình \(\left\{ \begin{array}{l}0 \le y \le 4\\x \ge 0\\x - y - 1 \le 0\\x + 2y - 10 \le 0\end{array} \right..\) Gọi điểm có toạ độ (x; y) thuộc miền nghiệm của hệ bất phương trình sao cho F(x; y) = x + 2y đạt giá trị lớn nhất. Số điểm thoả mãn là:
