A.
x | –3 | –2 | \[ - \frac{3}{2}\] | –1 | 0 |
f(x) | 8 | 2 | 1 | 2 | 8 |
B.
x | –3 | –2 | \[ - \frac{3}{2}\] | –1 | 0 |
f(x) | 4 | 6 | 5 | 4 | 6 |
C.
x | –3 | –2 | \[ - \frac{3}{2}\] | –1 | 0 |
f(x) | 4 | 2 | \(\frac{7}{4}\) | 2 | 4 |
D.
x | –3 | –2 | \[ - \frac{3}{2}\] | –1 | 0 |
f(x) | 2 | 4 | \(\frac{7}{4}\) | 2 | 4 |
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
Xét hàm số y = f(x) = x2 + 3x + 4.
• Với x = –3, ta có f(–3) = (–3)2 + 3.(–3) + 4 = 4.
• Với x = –2, ta có f(–2) = (–2)2 + 3.(–2) + 4 = 2.
• Với x = \[ - \frac{3}{2}\], ta có \(f\left( { - \frac{3}{2}} \right) = {\left( { - \frac{3}{2}} \right)^2} + 3.\left( { - \frac{3}{2}} \right) + 4 = \frac{7}{4}\).
• Với x = –1, ta có f(–1) = (–1)2 + 3.(–1) + 4 = 2.
• Với x = 0, ta có f(0) = 02 + 3.0 + 4 = 4.
Vậy bảng giá trị của hàm số đã cho là:
|
x |
–3 |
–2 |
\[ - \frac{3}{2}\] |
–1 |
0 |
|
f(x) |
4 |
2 |
\(\frac{7}{4}\) |
2 |
4 |
Do đó ta chọn đáp án C.
Cho hàm số y = f(x) = ax2 + bx + c có đồ thị như hình bên:
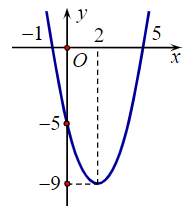
Trục đối xứng của đồ thị hàm số trên là đường thẳng:
Cho hàm số y = f(x) = ax2 + bx + c có đồ thị như hình vẽ:
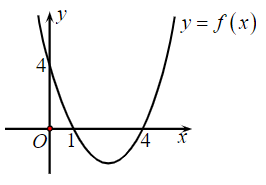
Đặt ∆ = b2 – 4ac. Tìm dấu của a và ∆.
