 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {a{x^2} + bx} - cx} \right) = - 2\)
\( \Leftrightarrow \mathop {\lim }\limits_{x \to + \infty } \frac{{a{x^2} + bx - {c^2}{x^2}}}{{\sqrt {a{x^2} + bx} + cx}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\left( {a - {c^2}} \right){x^2} + bx}}{{\sqrt {a{x^2} + bx} + cx}} = - 2\)
Điều này xảy ra nên \(\left\{ {\begin{array}{*{20}{c}}{a - {c^2} = 0\,\,(a,\,\,c > 0)}\\{\frac{b}{{\sqrt a + c}} = - 2\,\,(*)}\end{array}} \right..\)
Mặt khác ta cũng có c2 + a = 18.
Lập hệ phương trình ta có: \(\left\{ {\begin{array}{*{20}{c}}{ - {c^2} + a = 0}\\{{c^2} + a = 18}\end{array}} \right.\)
Û c2 = a = 9 Þ c = 3.
Thay a, c vào (*) Þ b = −12.
Vậy P = a + b + 5c = 12.
Tính các giới hạn sau.
A = lim\(\frac{{2{n^2} - n + 2}}{{3{n^2} + 5n}}\)
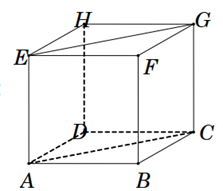
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính \(\overrightarrow {AB} .\overrightarrow {EG} \) bằng
Cho hình chóp S.ABC có SA ^ (ABC).
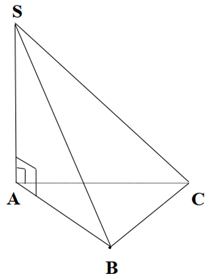
Góc giữa đường thẳng SC và mặt phẳng (ABC) là
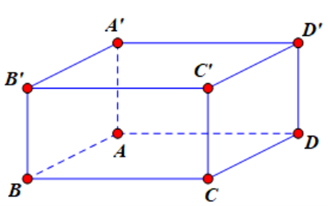
Cho hình lập phương ABCD.A’B’C’D’. Bộ ba vectơ nào sau đây đồng phẳng?
Cho hai hàm số f(x), g(x) thỏa mãn \(\mathop {\lim }\limits_{x \to 1} f(x)\)= −6 và \(\mathop {\lim }\limits_{x \to 1} g(x)\)= 3. Giá trị của \(\mathop {\lim }\limits_{x \to 1} \left[ {f(x) - g(x)} \right]\) bằng:
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \)và \(\overrightarrow {DH} \)?
Tổng S = 1 + \(\frac{1}{2}\)+ \(\frac{1}{4}\)+ … + \(\frac{1}{{{2^n}}}\)+ … có giá trị là
Cho hàm số y = f(x) = x2 – 2x + 4 có đồ thị (C)
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(3; 7)
Cho hàm số y = 2\(\sqrt x - x\)với x > 0. Tính y'(1) có kết quả là