Cho hai hàm số: và y=x-4 có đồ thị lần lượt là (P) và (d)
1) Vẽ hai đồ thị (P) và (d) trên cùng một mặt phẳng tọa độ.
 Giải bởi Vietjack
Giải bởi Vietjack
1) * Hàm số xác định với
Bảng giá trị:

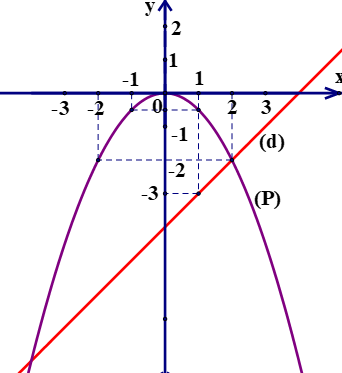
* Hàm số y=x-4 là đường thẳng đi qua các điểm có tọa độ (1;-3);(2;-2)
Đồ thị:
Tìm tất cả các giá trị của m để đường thẳng (d) cắt parabol tại hai điểm phân biệt có hoành độ lần lượt là (với ) sao cho .
Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y=2x-m+3 và parabol (P): .
1. Tìm m để đường thẳng (d) đi qua điểm A(2; 0).
a) Vẽ đồ thị (P) của hàm số và đường thẳng trên cùng một hệ trục tọa độ
Cho parabol và đường thẳng và đường thẳng Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có các hoành độ dương.
2. Cho điểm A thuộc (P) có hoành độ bằng 4. Tìm tham số m để đường thẳng (d): y=x-m đi qua A.
b) Tìm m để đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt A, B với sao cho
Cho parabol (P) :và đường thẳng (d) : .
1.Vẽ đồ thị (P).
2.Viết phương trình đường thẳng (d)biết () song song với (d) và () tiếp xúc với (P).
Cho phương trình: (m là tham số). Tìm m để phương trình có hai nghiệm thỏa mãn .
Tìm tất cả các giá trị m là số nguyên khác -1 sao cho giao điểm của đồ thị hai hàm số y=(m+2)x và có tọa độ là các số nguyên.
Tìm các giá trị của m để cả hai đường thẳng và cùng cắt trục hoành tại điểm có hoành độ .
Tìm các giá trị của m để phương trình có hai nghiệm phân biệt thỏa mãn điều kiện