Để xác định chiều cao của một tòa tháp mà không cần lên đỉnh của tòa nhà người ta làm như sau: đặt giác kế thẳng đứng cách chân tháp một khoảng AB = 55 m, chiều cao của giác kế là OA = 2 m.
Quay thanh giác kế sao cho khi ngắm theo thanh ta nhìn thấy đỉnh C của tháp. Đọc trên giác kế số đo góc COD=60.
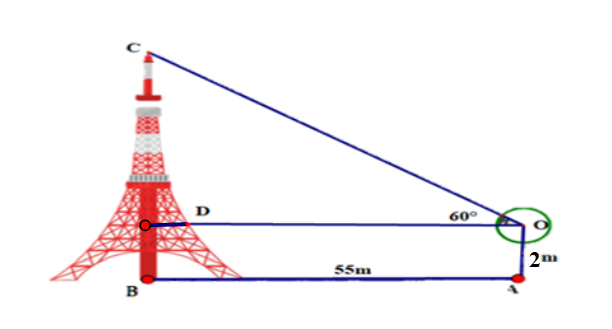
Chiều cao của ngọn tháo gần nhất với giá trị nào sau đây?
Giải bởi Vietjack
Đáp án đúng là: C
Xét tam giác OCD vuông tại D có OD = AB = 55 (m); COD=60.
Nên CD = OD. tanCOD = 55≈ 95,26 (m).
Vậy chiều cao của tháp là: 95,26 + 2 = 97,26 (m).
Xác định tập hợp B = {3; 6; 9; 12; 15} bằng cách nêu tính chất đặc trưng cho các phần tử của tập hợp.
Giá trị của biểu thức S = 2 + sin2 90° + 2cos2 60° − 3tan2 45° bằng:
Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 3x + 2y < 10?
Tam giác ABC có BC = 6, AC = 7, AB = 8. Bán kính đường tròn nội tiếp của tam giác ABC là
Cho các câu sau:
(1) Số 7 là số lẻ.
(2) Bài toán này khó quá!
(3) Cuối tuần này bạn có rảnh không?
(4) Số 10 là một số nguyên tố.
Trong các câu trên có bao nhiêu câu là mệnh đề?
Cho tam giác ABC có b = 7; c = 5, cosA =. Độ dài đường cao ha của tam giác ABC là
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
Bạn Vân có tối đa 120 phút để trồng rau trong vườn. Biết có hai loại rau là rau cải và rau muống, một cây rau cải trồng mất 5 phút, một cây rau muống trồng mất 7 phút. Gọi số cây rau cải bạn Vân trồng được là x cây, số cây rau muống bạn Vân trồng được là y cây. Các bất phương trình mô tả điều kiện của bài toán là:
