Giải bởi Vietjack
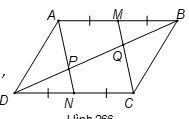
Áp dụng định nghĩa và giả thiết vào hình bình hành ,
ta được:
.
Tứ giác có hai cạnh đối song song và bằng nhau nên
nó là hình bình hành, do đó , suy ra
.
Áp dụng định lí Ta-lét vào hai tam giác và có , ta được:
(1).
(2)
Từ (1) và (2) ta có: .
Cho hình thang ABCD . Một đường thẳng song song với hai đáy, cắt các cạnh bên AD và BC theo thứ tự ở M và N.Chứng minh rằng:
Cho hình thang . Một đường thẳng song song với hai đáy, cắt các cạnh bên AD và BC theo thứ tự ở M và N. Chứng minh rằng:
