Hình thang cân ABCD ( AB// CD) , có góc C = 600, DB là tia phân giác của góc D; chu vi hình thang bằng 20cm.
a) Tính các cạnh của hình thang Giải bởi Vietjack
Giải bởi Vietjack
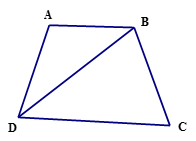
a) Ta có : ABCD là hình thang cân nên
; Tam giác CBD vuông tại B có => BC = DC hay 2AD = DC ;
AB // CD nên => ADB cân tại A nên AD = AB
Từ đó suy ra chu vi hình thang bằng 5AD => 5.AD = 20cm => AD = 4cm.
Vậy AD = AB = BC = 4cm, CD = 8cm
Cho ABC đều, điểm M nằm trong tam giác đó. Qua M, kẻ đường thẳng song song với AC và cắt BC ở E, kẻ đường thẳng song song với AB và cắt AC ở F, kẻ đường thẳng song song với BC và cắt AB ở D. CMR:
a) AFMD, BDME, CEMF là các hình thang cân.
Cho tam giác ABC cân tại A, M là điểm bất kì nằm giữa hai điểm A và B. Trên tia đối của tia CA lấy điểm N sao cho CN = BM. Vẽ ME và NF lần lượt vuông góc với đường thẳng BC. Gọi I là giao điểm của MN và BC.
a) Chứng minh: IE = IF.
Cho tứ giác ABCD có AD = AB = BC và . CMR:
a) Tia DB là phân giác của góc D.
Cho hình thang cân ABCD có , đáy nhỏ AD bằng cạnh bên của hình thang. Biết chu vi của hình thang bằng 20cm.
a) Tính các cạnh của hình thang.
Cho đều. Lấy điểm O nằm trong tam giác. Kẻ OI // AB (I thuộc AC), OM // BC (M thuộc AB), OK // AC (K thuộc BC). Chứng minh rằng: Chu vi bằng tổng khoảng cách từ O đến các đỉnh của
c) Điểm M phải ở vị trí nào để DEF là tam giác đều? Trong trường hợp này, tính chu vi của DEF theo chiều cao AH của ABC.