Cho tam giác ABC cân tại A, có M là trung điểm của BC. Kẻ tia Mx song song với AC cắt AB tại E và tia My song song với AB cắt AC tại F. Chứng minh:
a) EF là đường trung bình của tam giác ABC
Giải bởi Vietjack
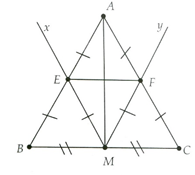
a) Mx đi qua trung điểm M của BC và song song với AC. Suy ra Mx đi qua trung điểm E của AB (theo Định lí 1).
Tương tự, ta được F cũng là trung điểm của AC. Khi đó EF trở thành đường trung bình của tam giác ABC;
Cho tam giác ABC. Gọi Bx và Cy lần lượt là các đường chứa tia phân giác của các góc ngoài tại đỉnh B và C. Gọi H và K lần lượt là hình chiếu của A trên Bx và Cy.
a) Chứng minh rằng tứ giác BCKH là hình thang;
Cho tam giác ABCcân tại A, đường cao AH và đường phân giác BD. Biết rằng , tính số đo các góc của tam giác ABC
Cho tam giác ABC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E. Gọi M, N lần lượt là trung điểm của BE và CD. Đường thẳng MN cắt tia AB và AC lần lượt là tại P và Q. Hỏi hai điểm D và E phải có điều kiện gì để tam giác APQ cân tại A?
