Giải bởi Vietjack
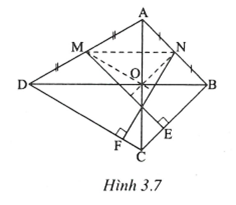
Gọi O là giao điểm của AC và BD.
Ta có: và OA = OC.
Xét có MN là đường trung bình
=> MN // BD và (vì ).
Xét có ON là đường trung bình
=> ON // BC và (vì ).
Xét có OM là đường trung bình
=> OM // CDvà (vì ).
Xét có OA, ME, NF là ba đường cao nên chúng đồng quy.
Cho tam giác ABC. Gọi Bx và Cy lần lượt là các đường chứa tia phân giác của các góc ngoài tại đỉnh B và C. Gọi H và K lần lượt là hình chiếu của A trên Bx và Cy.
a) Chứng minh rằng tứ giác BCKH là hình thang;
Cho tam giác ABCcân tại A, đường cao AH và đường phân giác BD. Biết rằng , tính số đo các góc của tam giác ABC
Cho tam giác ABC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E. Gọi M, N lần lượt là trung điểm của BE và CD. Đường thẳng MN cắt tia AB và AC lần lượt là tại P và Q. Hỏi hai điểm D và E phải có điều kiện gì để tam giác APQ cân tại A?
Cho tam giác ABC cân tại A, có M là trung điểm của BC. Kẻ tia Mx song song với AC cắt AB tại E và tia My song song với AB cắt AC tại F. Chứng minh:
a) EF là đường trung bình của tam giác ABC
