 Giải bởi Vietjack
Giải bởi Vietjack
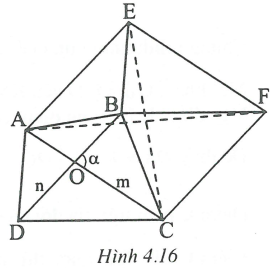
Xét tứ giác ABCD có và
Vẽ hình bình hành ADBE và vẽ hình bình hành CAEF.
Khi đó:
Như vậy hình bình hành CAEF hoàn toàn được xác định, do đó hai đường chéo AF và CE không đổi.
Dễ thấy tứ giác BFCD là hình bình hành => BF = CD
Chu vi tứ giác ABCD là:
Dấu ''='' xảy ra
<=> ABCD là hình bình hành.
Cho hình bình hành ABCD. Vẽ ra ngoài hình bình hành các tam giác ABM vuông cân tại A, tam giác BCN vuông cân tại C. Chứng minh rằng tam giác DMN vuông cân.
Cho hình bình hành ABCD (AD < AB) . Vẽ ra ngoài hình bình hành tam giác ABM cân tại B và tam giác ADN cân tại D sao cho
a) Chứng minh rằng CM = CN
Cho hình bình hành ABCD và đường thẳng xy không cắt các cạnh của hình bình hành. Qua các đỉnh A, B, C, D vẽ các đường thẳng vuông góc với xy, cắt xy lần lượt tại A', B', C', D'. Chứng minh rằng: AA' + CC' = BB' + DD'