 Giải bởi Vietjack
Giải bởi Vietjack
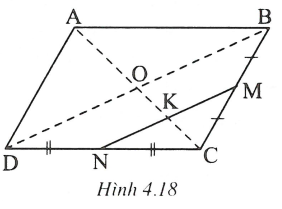
* Phân tích
Giả sử đã dựng được hình bình hành thỏa mãn đề bài.
Gọi O là giao điểm của hai đường chéo và K là giao điểm của MN và AC.
Xét có MN là đường trung bình, MN // BD
Xét có MB = MC và MK // OB nên CK = KO
Vậy MK là đường trung bình nên
Chứng minh tương tự, ta được
Mặt khác, OB = OD nên KM = KN
Vậy điểm K là trung điểm của MN xác định được.
Dễ thấy suy ra
Điểm C nằm trên tia đối của tia KA và cách K một khoảng
Điểm C xác định được thì các điểm B và D cũng xác định được.
* Cách dựng
- Dựng đoạn thẳng MN.
- Dựng trung điểm K của MN.
- Dựng tia AK.
- Trên tia đối của tia KA dựng điểm C sao cho
- Dựng điểm B sao cho M là trung điểm của CB.
- Dựng điểm D sao cho N là trung điểm của CD.
- Dựng các đoạn thẳng AB, AD ta được hình bình hành phải dựng.
Cho hình bình hành ABCD. Vẽ ra ngoài hình bình hành các tam giác ABM vuông cân tại A, tam giác BCN vuông cân tại C. Chứng minh rằng tam giác DMN vuông cân.
Cho hình bình hành ABCD (AD < AB) . Vẽ ra ngoài hình bình hành tam giác ABM cân tại B và tam giác ADN cân tại D sao cho
a) Chứng minh rằng CM = CN
Cho hình bình hành ABCD và đường thẳng xy không cắt các cạnh của hình bình hành. Qua các đỉnh A, B, C, D vẽ các đường thẳng vuông góc với xy, cắt xy lần lượt tại A', B', C', D'. Chứng minh rằng: AA' + CC' = BB' + DD'