Dạng 5. Bài tập nâng cao có đáp án
-
874 lượt thi
-
11 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
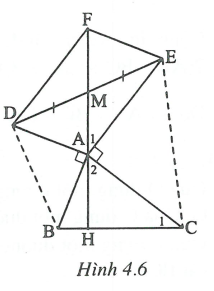
Vẽ hình bình hành DAEF. Khi đó AF đi qua M.
Gọi H là giao điểm của MA với BC.
Ta có:
mà nên
Ta có:
Do đó:
Câu 2:
Cho hình bình hành ABCD. Vẽ ra ngoài hình bình hành các tam giác ABM vuông cân tại A, tam giác BCN vuông cân tại C. Chứng minh rằng tam giác DMN vuông cân.
 Xem đáp án
Xem đáp án
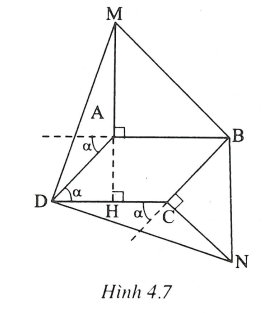
Ta đặt thì
và có:
Do đó
(1)
và
Kéo dài MA cắt CD tại H. Ta có:
Xét có
Hay (2)
Từ (1) và (2) suy ra vuông cân tại D
Câu 3:
 Xem đáp án
Xem đáp án
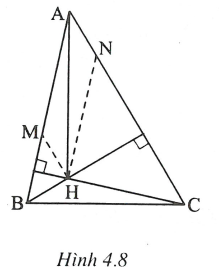
Vẽ
Vì nên . Vì nên
Xét vuông tại H có (1)
Xét vuông tại H có . (2)
Xét hình bình hành ANHM có
. (3)
Từ (1), (2), (3) suy ra:
do đó
hay
Chứng minh tương tự, ta được:
Cộng từng vế ba bất đẳng thức trên ta được:
Do đó
Câu 4:
 Xem đáp án
Xem đáp án
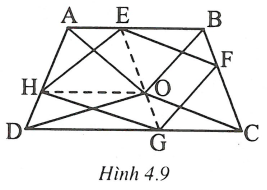
Qua O dựng một đường thẳng song song với BC cắt AB và CD lần lượt tại E và G. Qua O dựng một đường thẳng song song với CD cắt AD tại H.
Qua E dựng một đường thẳng song song với OC cắt BC tại F.
Khi đó tứ giác EFGH thỏa mãn đề bài.
Thật vậy, các tứ giác AEOH, HOGD là những hình thang cân.
=> OA = EH, OD = HG (1)
Tứ giác EFCO là hình bình hành => OC = EF (2)
và OE = CF. Suy ra OG = BF
Vậy tứ giác OBFG là hình bình hành => OB = GF (3)
Từ (1), (2), (3) suy ra tứ giác EFGH thỏa mãn đề bài.
Câu 5:
Cho hình bình hành ABCD và đường thẳng xy không cắt các cạnh của hình bình hành. Qua các đỉnh A, B, C, D vẽ các đường thẳng vuông góc với xy, cắt xy lần lượt tại A', B', C', D'. Chứng minh rằng: AA' + CC' = BB' + DD'
 Xem đáp án
Xem đáp án
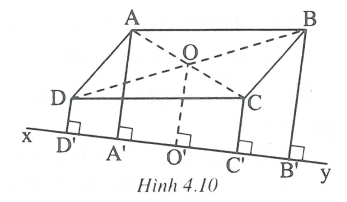
Gọi O là giao điểm của AC và BD. Vẽ
Ta có: AA' // BB' // CC' // DD' // OO'
Xét hình thang AA'C'C có OA = OC và OO' = AA' nên O'A' = O'C'
Do đó OO' là đường trung bình của hình thang hay AA' + CC' = 2OO'
Xét hình thang DD'B'B, cũng chứng minh tương tự, ta có: BB' + DD' = 2OO'
Từ đó suy ra: AA' + CC' = BB' + DD'Câu 6:
Cho hình bình hành ABCD (AD < AB) . Vẽ ra ngoài hình bình hành tam giác ABM cân tại B và tam giác ADN cân tại D sao cho
a) Chứng minh rằng CM = CN
 Xem đáp án
Xem đáp án
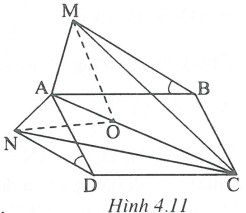
a) Vì ABCD là hình bình hành nên
Ta đặt khi đó
và có:
(chứng minh trên);
Vậy
Câu 7:
 Xem đáp án
Xem đáp án
b) Các và là những tam giác cân có góc ở đỉnh bằng nhau mà AB > AD nên AM > AN (bạn đọc tự chứng minh)
Xét và có CM = CN; CA chung và AM > AN nênCâu 8:
 Xem đáp án
Xem đáp án
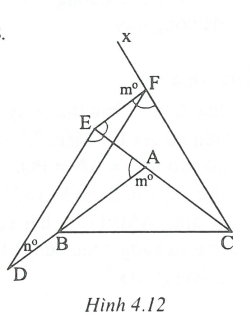
Qua A vẽ đường thẳng xy // PQ
Trên tia Ax lấy điểm M, trên tia Ay lấy điểm N sao cho AM = AN = PQ
Như vậy các điểm M và N cố định.
Tứ giác AMBD có hai cạnh đối diện song song và bằng nhau nên là hình bình hành => BM // AD
Mặt khác, BC // AD nên ba điểm B, M, C thẳng hàng (tiên đề Ơ-clit)
Do đó đường thẳng BC đi qua điểm cố định M.
Chứng minh tương tự, ta được đường thẳng CD đi qua điểm cố định N.Câu 9:
 Xem đáp án
Xem đáp án
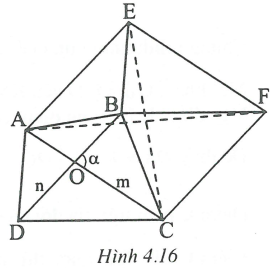
Xét tứ giác ABCD có và
Vẽ hình bình hành ADBE và vẽ hình bình hành CAEF.
Khi đó:
Như vậy hình bình hành CAEF hoàn toàn được xác định, do đó hai đường chéo AF và CE không đổi.
Dễ thấy tứ giác BFCD là hình bình hành => BF = CD
Chu vi tứ giác ABCD là:
Dấu ''='' xảy ra
<=> ABCD là hình bình hành.
Câu 10:
 Xem đáp án
Xem đáp án
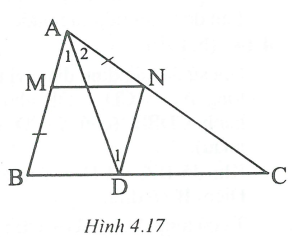
* Phân tích
Giả sử đã dựng được MN // BC sao cho BM = AN
Vẽ
Tứ giác MNDB là hình bình hành
=> DN = BM mà BM = AN nên DN = AN => cân
Mặt khác, (so le trong) nên
Do đó AD là đường phân giác của góc A.
Điểm D dựng được suy ra các điểm N và M cũng dựng được.
* Cách dựng
- Dựng đường phân giác AD của tam giác ABC.
- Dựng
- Dựng
Các bước còn lại, bạn đọc tự giải.
Câu 11:
 Xem đáp án
Xem đáp án
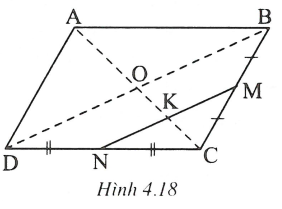
* Phân tích
Giả sử đã dựng được hình bình hành thỏa mãn đề bài.
Gọi O là giao điểm của hai đường chéo và K là giao điểm của MN và AC.
Xét có MN là đường trung bình, MN // BD
Xét có MB = MC và MK // OB nên CK = KO
Vậy MK là đường trung bình nên
Chứng minh tương tự, ta được
Mặt khác, OB = OD nên KM = KN
Vậy điểm K là trung điểm của MN xác định được.
Dễ thấy suy ra
Điểm C nằm trên tia đối của tia KA và cách K một khoảng
Điểm C xác định được thì các điểm B và D cũng xác định được.
* Cách dựng
- Dựng đoạn thẳng MN.
- Dựng trung điểm K của MN.
- Dựng tia AK.
- Trên tia đối của tia KA dựng điểm C sao cho
- Dựng điểm B sao cho M là trung điểm của CB.
- Dựng điểm D sao cho N là trung điểm của CD.
- Dựng các đoạn thẳng AB, AD ta được hình bình hành phải dựng.
