Giải bởi Vietjack
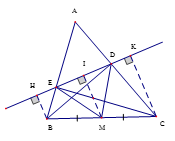
Vì BD, CE là các đường cao của ABC nên , do đó BDC vuông tại D, CEB vuông tại E.
Gọi M là trung điểm của BC, vẽ DM, EM thì DM, EM là các trung tuyến ứng với cạnh huyền của BDC và CEB.
Áp dụng tính chất đường trung tuyến ứng với cạnh huyền vào 2 tam giác vuông trên, ta được:
cân tại M
Từ giả thiết ta có tứ giác BKHC là hình thang vuông nên vẽ thêm thì BH // MI // CK (1)
Mà BM = MC (cách vẽ) (2)
Từ (1) và (2) suy ra BH, MI, CK là ba đường thẳng song song cách đều nên chúng chắn trên đường thẳng HK hai đoạn thẳng liên tiếp bằng nhau là HI = IK (3)
Ta có DM = EM suy ra MDE cân tại M , có MI là đường cao ứng vói cạnh đáy DE nên EI = ID (4)
Trừ theo vế đẳng thức (3) cho (4) ta được EH = DKCho góc vuông xOy và điểm A thuộc tia Ox sao cho OA = 4cm. lấy điểm B tùy ý trên tia Oy và gọi M là trung điểm của AB . Khi B di chuyển trên tia Oy thì M di chuyển trên đường nào
Cho tam giác ABC cân tại A, các điểm M, N theo thứ tự di động trên các cạnh AB, AC sao cho AM = CN. Hãy tìm tập hợp trung điểm I của MN
Cho điểm A nằm ngoài đường thẳng d . Điểm M di chuyển trên đường thẳng d . Gọi B là điểm đối xứng với A qua M. Điểm B di chuyển trên đường nào?
Cho điểm A ở ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. Trên d lấy một điểm B bất kì. Gọi C là điểm đối xứng với điểm A qua điểm B . Hỏi khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào?
Cho ABC có D là trung điểm của AB, kẻ DE // BC . Chứng minh rằng AE = EC.
