Cho hình thoi ABCD có AC cắt BD tại O. Lấy E đối xứng với A qua B. Gọi I, K lần lượt là giao điểm của DE với AC và BC; G là giao điểm của OE và BC; H là giao điểm của OK và CE. Chứng minh: A, G, H thẳng hàng.
 Giải bởi Vietjack
Giải bởi Vietjack
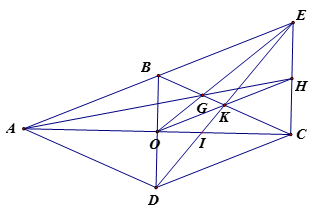
Vì ABCD là hình thoi
Vì E đối xứng với A qua B => AB = BE
=> là hình bình hành => KB = KC
ACE: là đường trung bình của ACE
=> OK // AB hay OH // AE
ACE: => H là trung điểm CE
Tam giác ACE có EO, CB là các đường trung tuyến => G là trọng tâm tam giác ACE
Mà H là trung điểm CE => A, G, H thẳng hàng.
Cho tam giác ABC cân tại A. Gọi D, E,F lần lượt là trung điểm của các cạnh BC, AB, AC. Chứng minh: tứ giác AEDF là hình thoi.
Cho ABC nhọn , đường cao tại AD, BE. Tia phân giác của cắt BE, BC theo thứ tự ở I, K.Tia phân giác của cắt AD, AC theo thứ tự ở M, N. Chứng minh: MINK là hình thoi.
Cho hình thoi ABCD . Trên AB, CD lấy E, F sao cho , . Gọi I là giao điểm của EF và DA, K là giao điểm của DE và BI. Chứng minh:
a) Tam giác BDI vuông.
Cho hình thoi ABCD có . Kẻ tại E, tại F, tại G, tại G, BE cắt DG tại M, BF cắt DH tại N. Chứng minh các góc của tứ giác BMDN bằng các góc của hình thoi ABCD.
Cho cân tại B. Đường thẳng qua C song song với AB cắt tia phân giác của tại D. Chứng minh: tứ giác ABCD là hình thoi.
Cho ABC cân tại A, đường cao AD. M là một điểm bất kì trên cạnh BC. Từ M vẽ ME vuông góc với AB tại E, MF vuông góc AC tại F. Gọi I là trung điểm của AM.
a) Chứng minh EID, DIF cân.
Cho ABC có AB < AC. Trên cạnh AC lấy D sao cho CD = AB. Gọi M, N lần lượt là trung điểm của AC, BD. Phân giác của cắt BC tại I. Chứng minh: .
Cho hình bình hành ABCD có . Gọi M, N theo thứ tự là trung điểm của AB, CD . Chứng minh tứ giác AMCN là hình thoi.
Cho hình thang ABCD (AB // CD) . Gọi M, N , P, Q lần lượt là trung điểm của AB, BC, CD, DA.
a) Chứng minh: MNPQ là hình bình hành.
Cho ABC cân tại B có đường cao BE. Trên tia đối của tia EB lấy điểm D sao cho ED = EB. Chứng minh: tứ giác ABCD là hình thoi.
Cho hình bình hành ABCD có và AD = 2.AB . Kẻ có Gọi M, N lần lượt là trung điểm của AD, BC. Chứng minh:
c) Với điều kiện của ABC ở câu b, gọi H là trực tâm của ABC. Chứng minh EF, ID, MH đồng quy.