Tập xác định của hàm số là:
A. ℝ;
B. (2; 6);
C. ∅;
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
Hàm số xác định khi và chỉ khi –2x2 + 8x – 12 > 0.
Tam thức bậc hai f(x) = –2x2 + 8x – 12 có ∆’ = 42 – (–2).(–12) = –8 < 0.
Do đó f(x) vô nghiệm.
Ta lại có a = –2 < 0.
Vì vậy f(x) < 0, với mọi x ∈ ℝ.
Vậy bất phương trình –2x2 + 8x – 12 > 0 có tập nghiệm là ∅.
Ta chọn phương án C.
Cho hàm số y = f(x) = ax2 + bx + c có đồ thị như hình vẽ.
Đặt ∆ = b2 – 4ac. Chọn khẳng định đúng?
Cho tam thức bậc hai f(x) = x2 + 1. Mệnh đề nào sau đây đúng nhất?
Cho tam thức bậc hai f(x) = –2x2 + 8x – 8. Trong các mệnh đề sau, mệnh đề nào đúng?
Cho hàm số y = f(x) có đồ thị như hình bên.
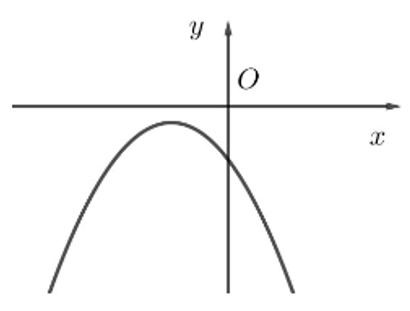
Bảng xét dấu của tam thức bậc hai tương ứng là:
Cho hàm số bậc hai f(x) có đồ thị như hình bên.
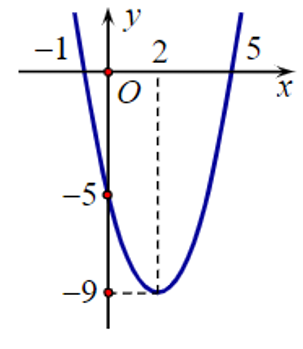
Tập nghiệm của bất phương trình f(x) ≥ 0 là:
Cho f(x) = –x2 – 4x + 5. Có bao nhiêu giá trị nguyên của x thỏa mãn f(x) ≥ 0?
Cho tam thức bậc hai f(x) = x2 – 10x + 2. Kết luận nào sau đây đúng?
