Cho hình thoi ABCD . Trên các cạnh BC và CD lần lượt lấy hai điểm E và F sao cho BE = DF. Gọi G, H thứ tự là giao điểm của AE, AF với đường chéo BD. Chứng minh rằng tứ giác AGCH là hình thoi.
 Giải bởi Vietjack
Giải bởi Vietjack
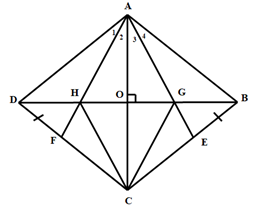
Gọi O là giao điểm của AC và BD khi đó (Vì O là giao điểm của hai đường chéo của hình thoi)
Xét và có:
AB = AD (Vì ABCD là hình thoi)
(Vì ABCD là hình thoi)
BE = DF (giả thiết)
Suy ra
Suy ra (hai góc tương ứng).
Mà AC là phân giác của
Do đó AO là phân giác của (*)
Xét có:
AO là đường cao, đồng thời là đường phân giác nên cân tại A.
Suy ra HO = OG (1)
Lại có AO = OC ( Vì ABCD là hình thoi có trung điểm O ) (2)
Từ (1) và (2) suy ra AGCH là hình bình hành. (**)
Từ (*) và (**) ta được tứ giác AGCH là hình thoi. (đpcm)
Cho hình chữ nhật ABCD . Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng tứ giác EFGH là hình thoi.
Cho tam giác ABC cân tại A . Đường thẳng qua B song song với AC cắt đường thẳng qua C song song với AB tại D. Chứng minh rằng tứ giác ABDC là hình thoi.
Cho tứ giác ABCD có AD = BC. Gọi E, F, M, N lần lượt là trung điểm của AB, DC, DB, AC. Chứng minh tứ giác EFMN là hình thoi.
Cho hình bình hành ABCD có AB = 2.AD. Gọi M, N lần lượt là trung điểm cạnh CD, AB. Chứng minh tứ giác ANMD là hình thoi.