Giải bởi Vietjack
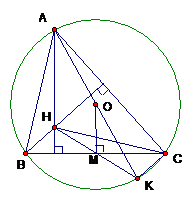
OM vuông góc với BC => M trung điểm của BC
(định lý đường kính và dây cung) => M là trung điểm của HK (vì BHCK là hình bình hành) => đpcm tam giác AHK có OM là đường trung bình => AH = 2.OM
Cho hình bình hành ABCD có đỉnh D nằm trên đường tròn đường kính AB = 2R. Hạ BN và DM cùng vuông góc với đường chéo AC.Chứng minh tứ giác: CBMD nội tiếp được
Cho đường tròn (O), đường kính AB cố định, điểm I nằm giữa A và O sao cho AI = AO. Kẻ dây MN vuông góc với AB tại I. Gọi C là điểm tùy ý thuộc cung lớn MN sao cho C không trùng với M, N và. B Nối AC cắt MN tại E.
Chứng minh ∆AME ∆ACM và = AE.AC
Chứng minh AM. BN =
Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax, By lần lượt ở C và D. Các đường thẳng AD và BC cắt nhau tại N.
Chứng minh AC + BD = CD
Trên đoạn thẳng AB cho điểm C nằm giữa A và B Trên cùng một nửa mặt phẳng có bờ là AB kẻ hai tia Ax và By cùng vuông góc với AB Trên tia Ax lấy điểm I, tia vuông góc với CI tại C cắt tia By tại K. Đường tròn đường kính IC cắt IK tại P ( P khác I)
Chứng minh tứ giác CPKB nội tiếp một đường tròn, chỉ rõ đường tròn này.
Xác định vị trí của điểm M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị lớn nhất.
Cho hình bình hành ABCD có đỉnh D nằm trên đường tròn đường kính AB = 2R. Hạ BN và DM cùng vuông góc với đường chéo AC. Chứng minh rằng: DBDC = DN.AC
Trên đoạn thẳng AB cho điểm C nằm giữa A và B Trên cùng một nửa mặt phẳng có bờ là AB kẻ hai tia Ax và By cùng vuông góc với AB Trên tia Ax lấy điểm I, tia vuông góc với CI tại C cắt tia By tại K. Đường tròn đường kính IC cắt IK tại P ( P khác I)
Cho đường tròn (O), dây AB không đi qua tâm. Trên cung nhỏ AB lấy điểm M (M không trùng với A, B). Kẻ dây MN vuông góc với AB tại H. Kẻ MK vuông góc với AN .
Cho đường tròn (O), dây AB không đi qua tâm. Trên cung nhỏ AB lấy điểm M (M không trùng với A, B). Kẻ dây MN vuông góc với AB tại H. Kẻ MK vuông góc với AN .
Cho đường tròn (O) đường kính AB Gọi I là trung điểm của OA Vẽ đường tron tâm I đi qua A, trên (I) lấy P bất kì, AP cắt (O) tại Q. Xác định vị trí của P để tam giác AQB có diện tích lớn nhất.
Cho (O),dây cung AB. Từ điểm M bất kỳ trên cung AB sao cho MA> MB (M¹A và M¹B), kẻ dây cung MN vuông góc với AB tại H. Gọi MQ là đường cao của tam giác MAN.
Cho (O),dây cung AB. Từ điểm M bất kỳ trên cung AB sao cho MA> MB (M¹A và M¹B), kẻ dây cung MN vuông góc với AB tại H. Gọi MQ là đường cao của tam giác MAN.
C/m 4 điểm A;M;H;Q cùng nằm trên một đường tròn.
Cho đường tròn (O) đường kính AB Gọi I là trung điểm của OA Vẽ đường tron tâm I đi qua A, trên (I) lấy P bất kì, AP cắt (O) tại Q. Chứng minh IP // OQ.
Cho đường tròn (O) đường kính AB cố định và đường kính CD thay đổi không trùng với AB Tiếp tuyến tại A của đường tròn (O) cắt các đường thẳng BC và BD lần lượt tại E và F. Gọi P và Q lần lượt là trung điểm của các đoạn thẳng AE và AF.
Xác định vị trí của đường kính CD để tam giác BPQ có diện tích nhỏ nhất.
