Cho đường tròn , đường kính BC, A là điểm trên đường tròn ( A khác B và C). Kẻ AH vuông góc với BC (H thuộc BC). Đường tròn tâm I đường kính AH cắt AB,AC và đường tròn (O) tại . Chứng minh OA vuông góc với DE
 Giải bởi Vietjack
Giải bởi Vietjack
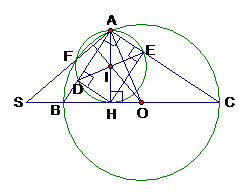
Chứng minh :
Ta có: cân tại O ()
. Mà ( vuông tại A)
hay
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O;R). H là trực tâm của tam giác ABC. Vẽ đường kính AD của đường tròn (O) ; vẽ tại M. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng H,G,O thẳng hàng và .
Cho tam giác ABC vuông ở A. Trên cạnh AC lấy điểm M, dựng đường tròn (O) có đường kính MC. đường thẳng BM cắt đường tròn (O) tại. D. đường thẳng AD cắt đường tròn (O) tại S. Chứng minh điểm M là tâm đường tròn nội tiếp tam giác ADE.
Cho tam giác ABC vuông ở A. Trên cạnh AC lấy điểm M, dựng đường tròn (O) có đường kính MC. đường thẳng BM cắt đường tròn (O) tại. D. đường thẳng AD cắt đường tròn (O) tại S.Chứng minh ABCD là tứ giác nội tiếp.
Cho tam giác ABC vuông ở A. Trên cạnh AC lấy điểm M, dựng đường tròn (O) có đường kính MC. đường thẳng BM cắt đường tròn (O) tại. D. đường thẳng AD cắt đường tròn (O) tại S. Chứng minh CA là tia phân giác của góc SCB.
Hai đường tròn (O;R) và (O';r) tiếp xúc ngoài tại gọi AC và BC là hai đường kính đi qua C của đường tròn (O) và (O'). DE là dây cung của đường tròn (O) vuông góc với AB tại trung điểm M của AB. Tia DC cắt đường tròn (O') tại điểm thứ 2 là F. Chứng minh MF là tiếp tuyến của (O')
Cho tam giác ABC vuông ở A. Trên cạnh AC lấy điểm M, dựng đường tròn (O) có đường kính MC. đường thẳng BM cắt đường tròn (O) tại. D. đường thẳng AD cắt đường tròn (O) tại S. Chứng minh DM là tia phân giác của góc ADE.
Cho tam giác ABC vuông tại A,I là một điểm trên cạnh AC. Đường tròn đường kính IC cắt BC ở E và cắt BI ở D. Chứng minh I là tâm đường tròn nội tiếp tam giác ADE.
Cho đường tròn (O) đường kính AB. Trên đoạn thẳng OB lấy điểm H bất kì ( H không trùng O, B); trên đường thẳng vuông góc với OB tại H, lấy một điểm M ở ngoài đường tròn; MA và MB thứ tự cắt đường tròn (O) tại C và D. Gọi I là giao điểm của AD và BC. Chứng minh các đường thẳng AD, BC, MH đồng quy tại I.
Hai đường tròn và tiếp xúc ngoài tại gọi AC và BC là hai đường kính đi qua C của đường tròn (O) và (O'). DE là dây cung của đường tròn (O) vuông góc với AB tại trung điểm M của AB. Tia DC cắt đường tròn (O') tại điểm thứ 2 là F. DB cắt đường tròn (O') tại điểm thứ hai là G. Chứng minh DF, EG và AB đồng quy
Cho tam giác ABC vuông tại A và một điểm D nằm giữa A và B. Đường tròn (O) đường kính BD cắt BC tại E. Các đường thẳng CD, AE lần lượt cắt đường tròn (O) tại các điểm thứ hai là F, G. Chứng minh rằng : AC, DE và BF đồng quy.
Cho tam giác nhọn ABC nội tiếp đường tròn (O;R). Tiếp tuyến tại B và C của đường tròn (O;R) cắt nhau tại T, đường thẳng AT cắt đường tròn tại điểm thứ hai là D khác A. Chứng minh rằng
Cho ∆ABC (AC > AB, ). Gọi I, K theo thứ tự là trung điểm của AB, AC. Các đường tròn đường kính AB, AC cắt nhau tại điểm thứ hai D; tia BA cắt đường tròn (K) tại điểmt hứ hai E; tia CA cắt đường tròn (I) tại điểm thứ hai F.Chứng minh ba đường thẳng AD, BF, CE đồng quy.
Từ một điểm C ở ngoài đường tròn (O) kẻ các tuyến CBA . Gọi IJ là đường kính vuông góc với AB. Các đường thẳng theo thứ tự cắt đường tròn (O) tại . Chứng minh rằng đồng quy tại một điểm D.
Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm M không trùng với A và C. Vẽ đường tròn đường kính MC, cắt cạnh BC tại M. Các đường thẳng BM và AD lần lượt cắt đường tròn tại các điểm E,F. Chứng minh rằng: Các đường thẳng đồng quy.
Cho ∆ABC (AC > AB, ). Gọi I, K theo thứ tự là trung điểm của AB, AC. Các đường tròn đường kính AB, AC cắt nhau tại điểm thứ hai D; tia BA cắt đường tròn (K) tại điểmt hứ hai E; tia CA cắt đường tròn (I) tại điểm thứ hai F.Gọi H là giao điểm thứ hai của tia DF với đường tròn ngoại tiếp tam giác AEF, hãy so sánh DH và DE.