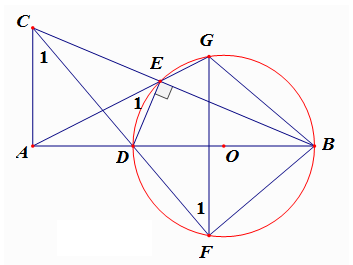
Dạng 2: Lợi dụng các đường đồng quy trong tam giác: đồng quy tại trực tâm, trọng tâm, tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác có đáp án
-
645 lượt thi
-
40 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Từ một điểm C ở ngoài đường tròn (O) kẻ các tuyến CBA . Gọi IJ là đường kính vuông góc với AB. Các đường thẳng theo thứ tự cắt đường tròn (O) tại . Chứng minh rằng đồng quy tại một điểm D.
 Xem đáp án
Xem đáp án

D thuộc đường tròn đường kính IJ nên hay
Tương tự
Tam giác có 3 đường cao đồng quy tại D.
Vậy đồng quy tại một điểm D.
Câu 2:
Cho tam giác ABC vuông ở A. Trên cạnh AC lấy điểm M, dựng đường tròn (O) có đường kính MC. đường thẳng BM cắt đường tròn (O) tại. D. đường thẳng AD cắt đường tròn (O) tại S.Chứng minh ABCD là tứ giác nội tiếp.
 Xem đáp án
Xem đáp án
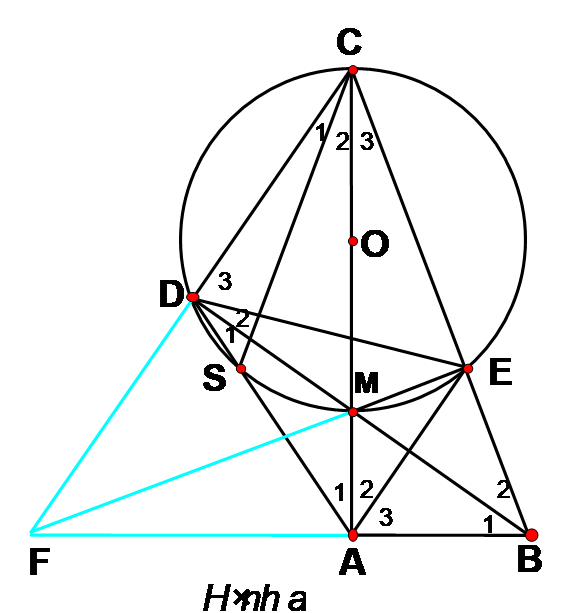
Câu 3:
Cho tam giác ABC vuông ở A. Trên cạnh AC lấy điểm M, dựng đường tròn (O) có đường kính MC. đường thẳng BM cắt đường tròn (O) tại. D. đường thẳng AD cắt đường tròn (O) tại S. Chứng minh CA là tia phân giác của góc SCB.
 Xem đáp án
Xem đáp án
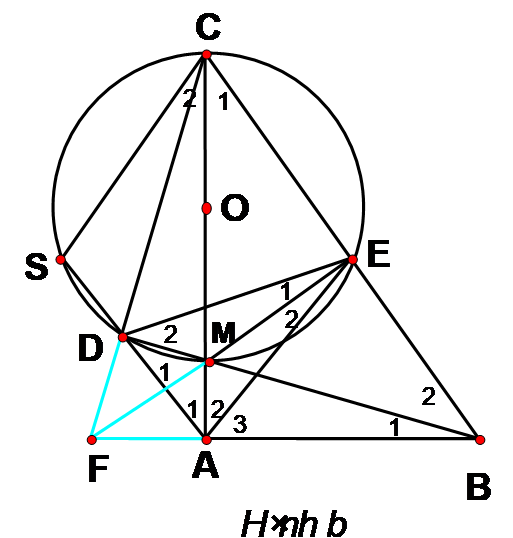
ABCD là tứ giác nội tiếp => ( nội tiếp cùng chắn cung AB).
=> => (hai góc nội tiếp đường tròn (O) chắn hai cung bằng nhau) => CA là tia phân giác của góc SCB.
TH2 (Hình b)
(cùng phụ ACB ); (cùng bù ADC ) =>
=> => => CA là tia phân giác của góc SCB.
Câu 4:
Cho tam giác ABC vuông ở A. Trên cạnh AC lấy điểm M, dựng đường tròn (O) có đường kính MC. đường thẳng BM cắt đường tròn (O) tại. D. đường thẳng AD cắt đường tròn (O) tại S. Gọi E là giao điểm của BC với đường tròn (O). Chứng minh rằng các đường thẳng BA, EM, CD đồng quy.
 Xem đáp án
Xem đáp án
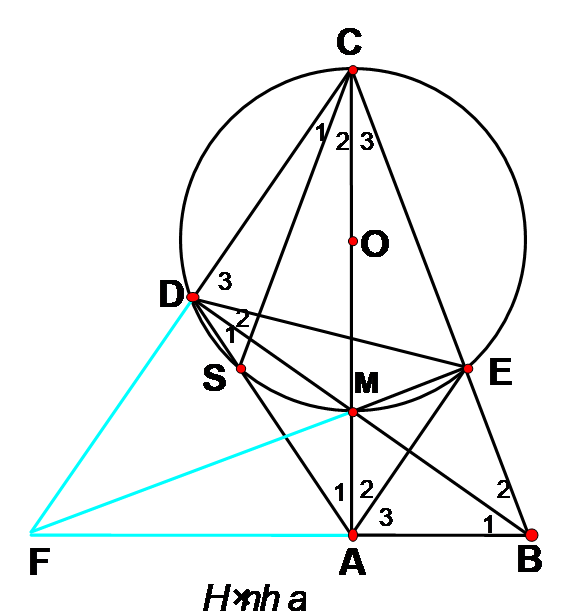
Xét DCMB Ta có BA^CM; CD ^ BM; ME ^ BC như vậy BA, EM, CD là ba đường cao của tam giác CMB nên BA, EM, CD đồng quy.
Câu 5:
Cho tam giác ABC vuông ở A. Trên cạnh AC lấy điểm M, dựng đường tròn (O) có đường kính MC. đường thẳng BM cắt đường tròn (O) tại. D. đường thẳng AD cắt đường tròn (O) tại S. Chứng minh DM là tia phân giác của góc ADE.
 Xem đáp án
Xem đáp án
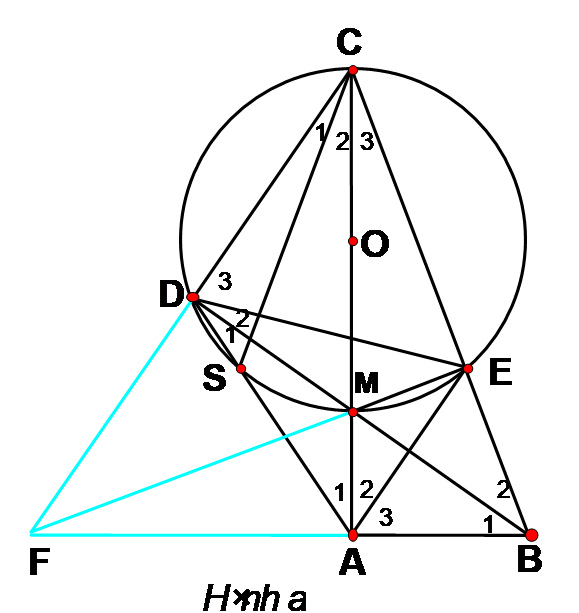
Theo trên Ta có => => DM là tia phân giác của góc ADE.(1)
Câu 6:
Cho tam giác ABC vuông ở A. Trên cạnh AC lấy điểm M, dựng đường tròn (O) có đường kính MC. đường thẳng BM cắt đường tròn (O) tại. D. đường thẳng AD cắt đường tròn (O) tại S. Chứng minh điểm M là tâm đường tròn nội tiếp tam giác ADE.
 Xem đáp án
Xem đáp án
Ta có (nội tiếp chắn nửa đường tròn (O)) => .
Tứ giác AMEB có ; => mà đây là hai góc đối nên tứ giác AMEB nội tiếp một đường tròn =>
Tứ giác ABCD là tứ giác nội tiếp => ( nội tiếp cùng chắn cung CD)
=> => AM là tia phân giác của góc DAE (2)
Từ (1) và (2) ta có M là tâm đường tròn nội tiếp tam giác ADE.
Câu 7:
Cho đường tròn (O) đường kính AB. Trên đoạn thẳng OB lấy điểm H bất kì ( H không trùng O, B); trên đường thẳng vuông góc với OB tại H, lấy một điểm M ở ngoài đường tròn; MA và MB thứ tự cắt đường tròn (O) tại C và D. Gọi I là giao điểm của AD và BC. Chứng minh MCID là tứ giác nội tiếp.
 Xem đáp án
Xem đáp án
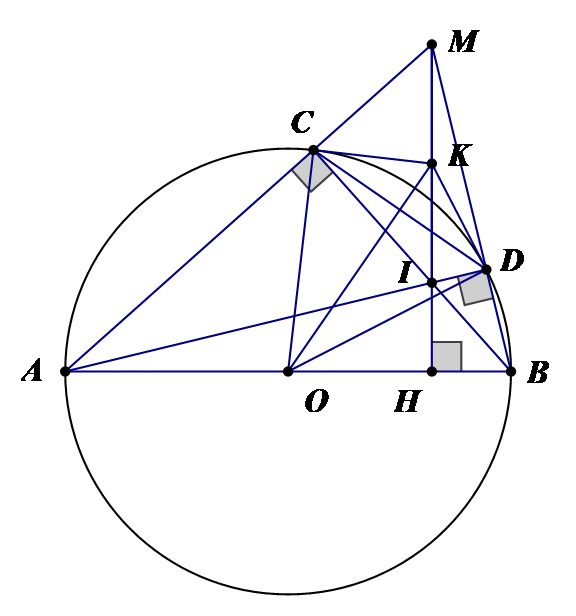
( nội tiếp chắn nửa đường tròn ) ….
=> mà đây là hai góc đối của tứ giác MCID nên MCID là tứ giác nội tiếp.
Câu 8:
Cho đường tròn (O) đường kính AB. Trên đoạn thẳng OB lấy điểm H bất kì ( H không trùng O, B); trên đường thẳng vuông góc với OB tại H, lấy một điểm M ở ngoài đường tròn; MA và MB thứ tự cắt đường tròn (O) tại C và D. Gọi I là giao điểm của AD và BC. Chứng minh các đường thẳng AD, BC, MH đồng quy tại I.
 Xem đáp án
Xem đáp án
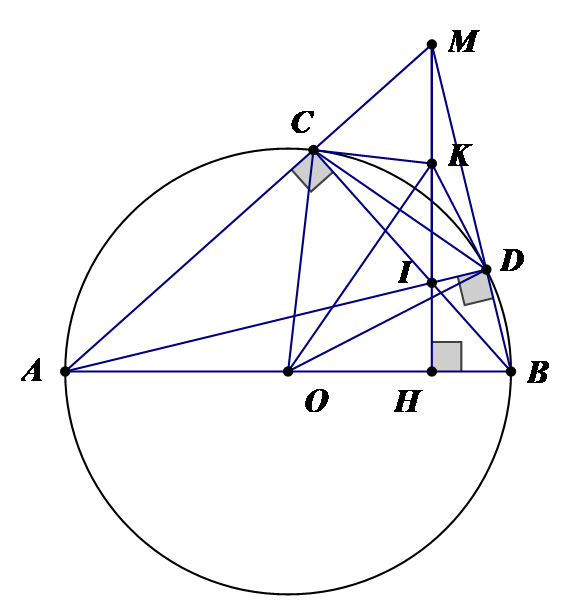
AD, MC, MH là ba đường cao của tam giác BAM nên đồng quy tại I.
Câu 9:
Cho đường tròn (O) đường kính AB. Trên đoạn thẳng OB lấy điểm H bất kì ( H không trùng O, B); trên đường thẳng vuông góc với OB tại H, lấy một điểm M ở ngoài đường tròn; MA và MB thứ tự cắt đường tròn (O) tại C và D. Gọi I là giao điểm của AD và BC. Gọi K là tâm đường tròn ngoại tiếp tứ giác MCID, Chứng minh KCOH là tứ giác nội
 Xem đáp án
Xem đáp án
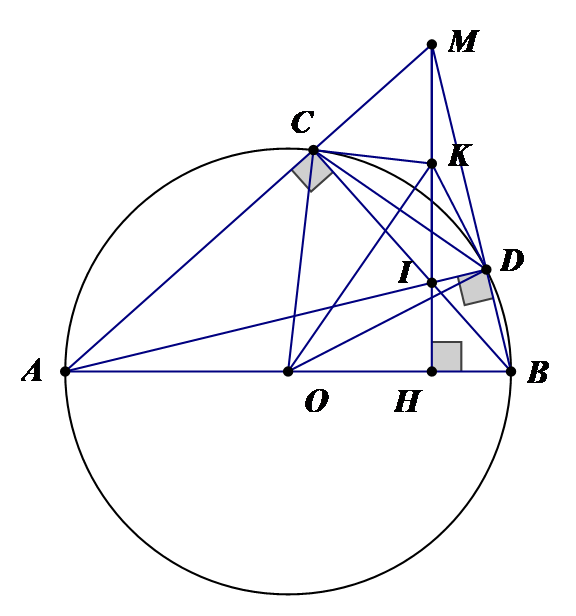
Chỉ ra KCI là tam giác cân, từ đó
. Từ đó chỉ ra …. (tự chứng minh)
Câu 10:
Cho tam giác nhọn ABC nội tiếp đường tròn (O;R). Tiếp tuyến tại B và C của đường tròn (O;R) cắt nhau tại T, đường thẳng AT cắt đường tròn tại điểm thứ hai là D khác A. Chứng minh rằng
 Xem đáp án
Xem đáp án
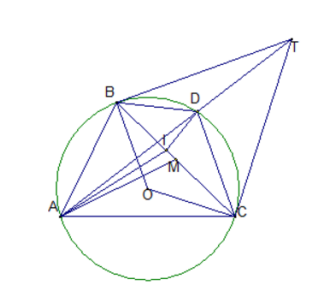
Xét tam giác ABT và tam giác BDT có:
BTD chung
(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cùng chắn cung BD).
=> (g-g)
Câu 11:
Cho tam giác nhọn ABC nội tiếp đường tròn (O;R). Tiếp tuyến tại B và C của đường tròn (O;R) cắt nhau tại T, đường thẳng AT cắt đường tròn tại điểm thứ hai là D khác A. Chứng minh rằng : AB.CD = BD.AC
 Xem đáp án
Xem đáp án
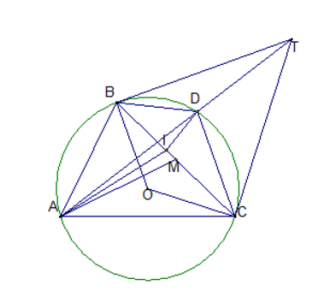
Có (g-g)
Chứng minh được (g-g)
Tiếp tuyến tại B và C cắt nhau tại T nên BT = CT (3)
Từ (1), (2), (3) có
Câu 12:
Cho tam giác nhọn ABC nội tiếp đường tròn (O;R). Tiếp tuyến tại B và C của đường tròn (O;R) cắt nhau tại T, đường thẳng AT cắt đường tròn tại điểm thứ hai là D khác A. Chứng minh rằng hai đường phân giác góc BAC; BDC và đường thẳng BC đồng quy tại một điểm
 Xem đáp án
Xem đáp án
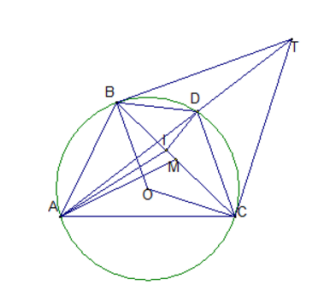
Phân giác góc BAC cắt BC tại I, theo tính chất phân giác trong tam giác ta có:
Từ AB.CD = BD.AC
=> DI là phân giác góc BDC
Do đó hai đường phân giác góc BAC và BDC và đường thẳng BC đồng quy.
Câu 13:
Cho nửa đường tròn ( O) đường kính AB. Vẽ 2 tiếp tuyến Ax và By. Lấy M trên đường tròn sao cho AM < BM. AM cắt By tại F, BM cắt Ax tại E. Chứng minh:
 Xem đáp án
Xem đáp án
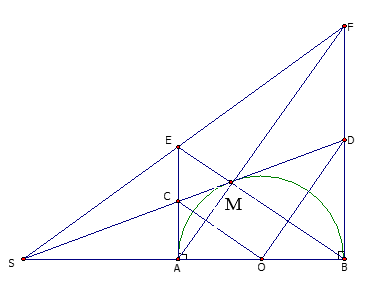
Ta có = 90º (góc nội tiếp chắn nửa đường tròn) AM BE
Xét ∆EAB và ∆ABF có:
(cùng phụ với )
Suy ra ∆EAB ~ ∆ABF ( g.g)
AB2 = AE. BF
Câu 14:
Cho nửa đường tròn ( O) đường kính AB. Vẽ 2 tiếp tuyến Ax và By. Lấy M trên đường tròn sao cho AM < BM. AM cắt By tại F, BM cắt Ax tại E. Tiếp tuyến của đường tròn tại M cắt AE, BF tại C và D. Chứng minh C và D là trung điểm của AE và BF.
 Xem đáp án
Xem đáp án
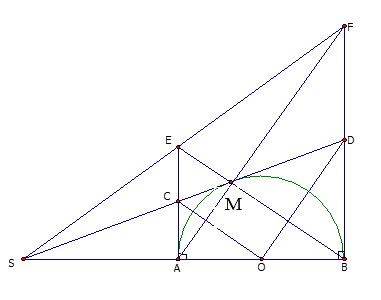
CA = CM và CO là tia phân giác của ACM
∆AMC cân tại C và CO là đường cao CO AM
Do đó trong ∆ABE có OA=OB, OC//BE nên CA=CE.
Câu 15:
Cho nửa đường tròn ( O) đường kính AB. Vẽ 2 tiếp tuyến Ax và By. Lấy M trên đường tròn sao cho AM < BM. AM cắt By tại F, BM cắt Ax tại E. Chứng minh các đường thẳng AB, CD, EF đồng quy.
 Xem đáp án
Xem đáp án
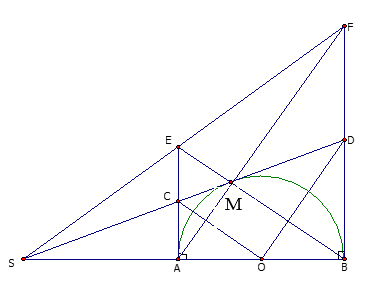
Gọi giao điểm của AB và EF là S. Ta sẽ chứng minh S, C, D thằng hàng.
Giả sử SC cắt BF tại D’. Vì AE // BF nên theo định lí Ta-let, có:
D’ là trung điểm của BF
D trùng với D’ hay S, C, D thẳng hàng.
Vậy ba đường thẳng AB, EF, CD đồng quy tại S.
Câu 16:
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O;R). H là trực tâm của tam giác ABC. Vẽ đường kính AD của đường tròn (O) ; vẽ tại M. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng H,G,O thẳng hàng và .
 Xem đáp án
Xem đáp án
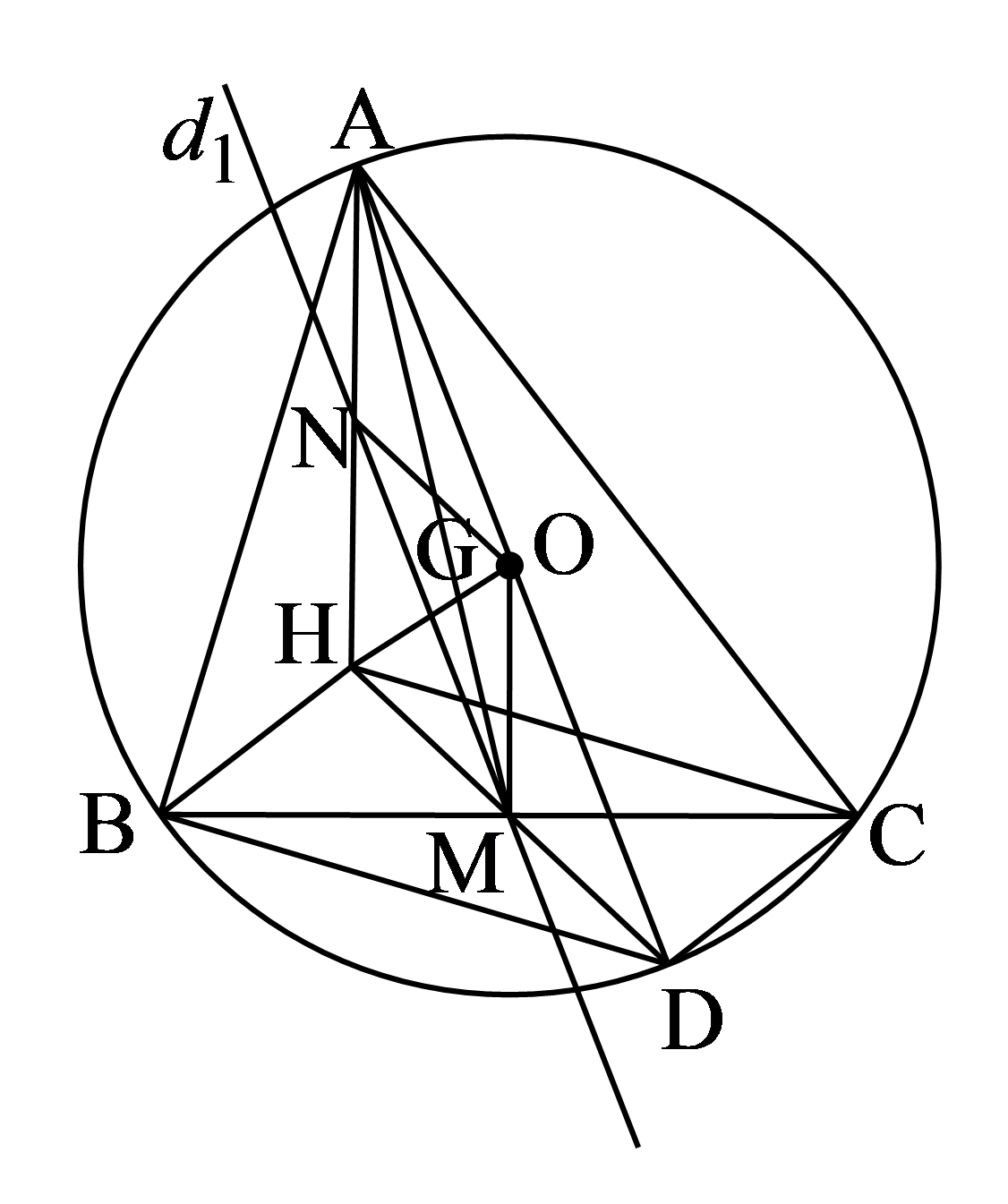
có AM là đường trung tuyến,G thuộc đoạn thẳng AM và nên G là trọng tâm của tam giác AHD .HO là đường trung tuyến nên đi qua G và
Câu 17:
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O;R). H là trực tâm của tam giác ABC. Vẽ đường kính AD của đường tròn (O) ; vẽ tại M.Gọi B',C' lần lượt là trung điểm của các cạnh CA,AB . Đường thẳng qua M song song với OA, đường thẳng qua B' song song với OB, đường thẳng qua C' song song với OC .Chứng minh rằng các đường thẳng đồng qui.
 Xem đáp án
Xem đáp án
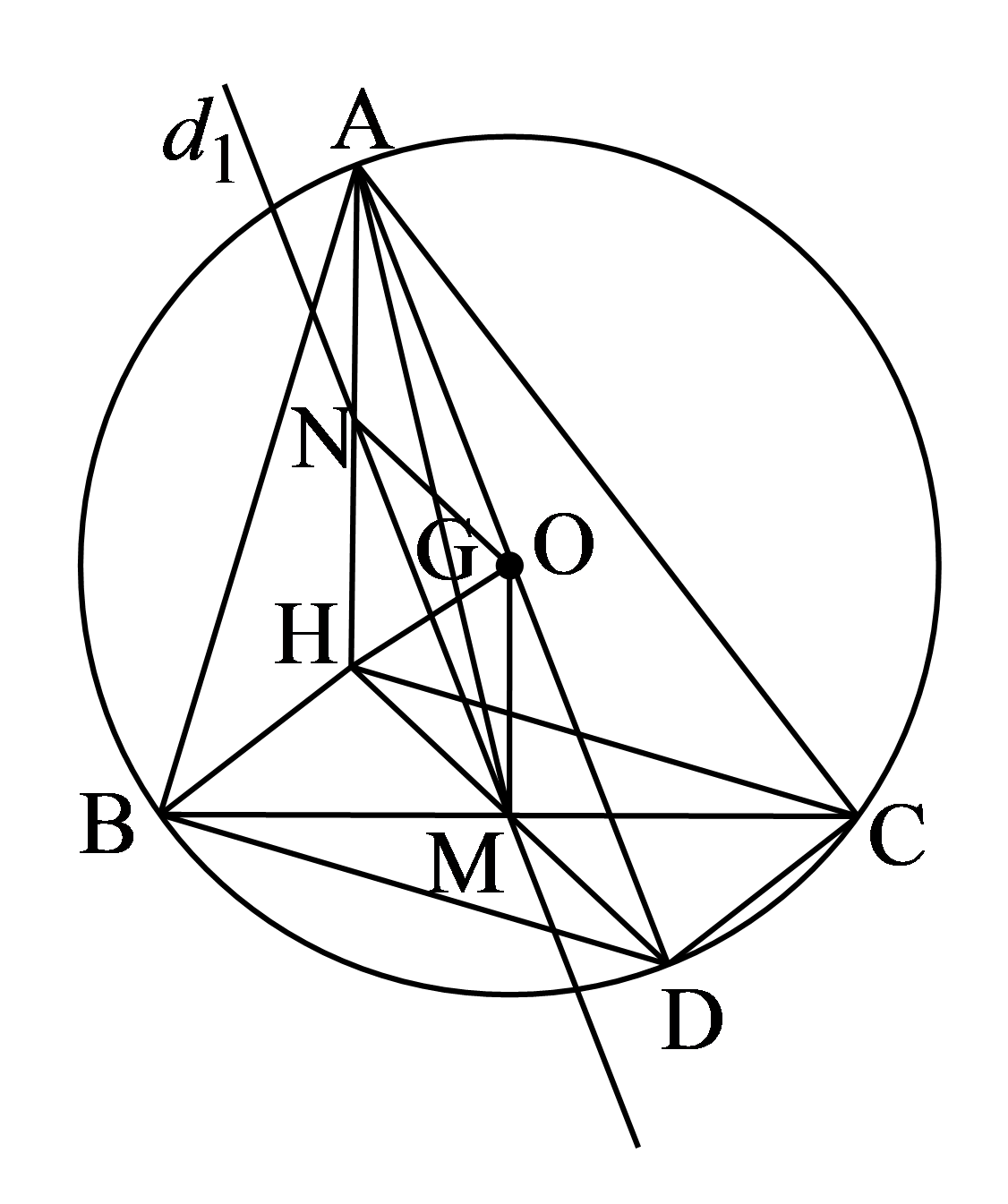 Gọi N là giao điểm của với AH
Gọi N là giao điểm của với AH
có , M là trung điểm của HD
là trung điểm của AH
Ta có:
Do đó HNOM là hình bình hành.
đi qua trung điểm I của OH
Chứng minh tương tự có đi qua I
Vậy các đường thẳng đồng quy
Câu 18:
 Xem đáp án
Xem đáp án
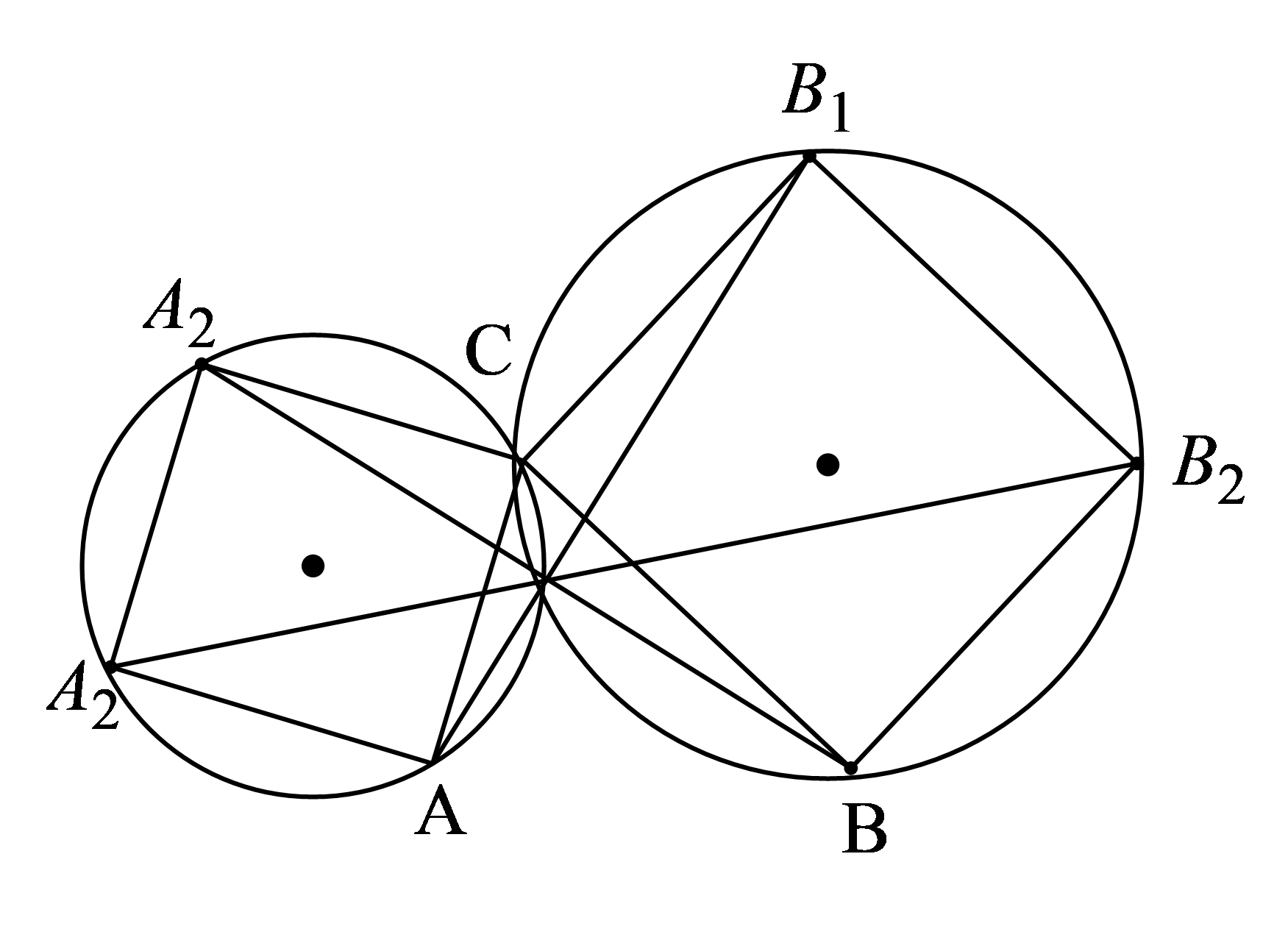
Trường hợp 1:. Rõ ràng đồng quy tại C.
Trường hợp 2:
Các đường tròn ngoại tiếp hình vuông và
Có điểm chung c sẽ cắt nhau tại M (khác )
Ta có: (góc nội tiếp chắn cung một phần tư đường tròn)
(góc nội tiếp chắn nửa đường tròn)
Tương tự:
Vì tia nằm giữa hai tia MA và MC,tia MC nằm giữa hai tia MB và
nên
hay thẳng hàng.
Chứng minh tương tự và thẳng hàng
Vậy và cùng đi qua M
Hay và đồng quy.
Câu 19:
Cho đường tròn (O;R) , đường kính BC, A là điểm trên đường tròn ( khác và ). Kẻ AH vuông góc với BC (H thuộc BC). Đường tròn tâm I đường kính AH cắt AB,AC và đường tròn (O) tại . Chứng minh tứ giác BDEC nội tiếp
 Xem đáp án
Xem đáp án
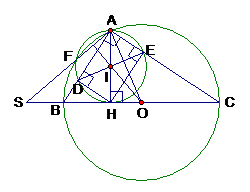
Chứng minh tứ giác BDEC nội tiếp:
Ta có: (góc nội tiếp chắn nửa đường tròn)
Ta lại có: (góc nội tiếp cùng chắn cung AE)
(cùng phụ với EHC )
Vậy tứ giác BDEC nội tiếp (góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện)
Câu 20:
Cho đường tròn , đường kính BC, A là điểm trên đường tròn ( A khác B và C). Kẻ AH vuông góc với BC (H thuộc BC). Đường tròn tâm I đường kính AH cắt AB,AC và đường tròn (O) tại . Chứng minh OA vuông góc với DE
 Xem đáp án
Xem đáp án
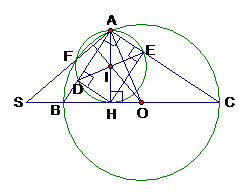
Chứng minh :
Ta có: cân tại O ()
. Mà ( vuông tại A)
hay
Câu 21:
Cho đường tròn (O;R), đường kính BC, A là điểm trên đường tròn ( A khác B và C). Kẻ AH vuông góc với BC ( H thuộc BC). Đường tròn tâm I đường kính AH cắt AB,AC và đường tròn (O) tại D,E,F. Chứng minh các đường thẳng đồng quy
 Xem đáp án
Xem đáp án
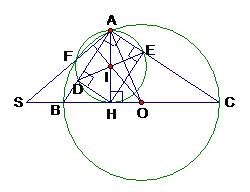
Chứng minh các đường thẳng đồng quy:
Gọi S là giao điểm của AF và BC
có: (gt)
(tính chất đường nối tâm của 2 đtr cắt nhau)
(đường cao thứ ba trong )
Mà (câu b)
thẳng hàng hay đường thẳng qua .
Vậy các đường thẳng đồng quy
Câu 22:
Cho đường tròn (O;R), đường kính BC, A là điểm trên đường tròn ( A khác B và C). Kẻ AH vuông góc với BC (H thuộc BC). Đường tròn tâm I đường kính AH cắt AB,AC và đường tròn (O) tại . Cho biết sđ . Tính theo R diện tích tứ giác BDEC
 Xem đáp án
Xem đáp án
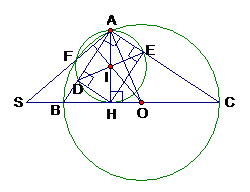
Tính theo R diện tích tứ giác BDEC:
Ta có: vuông tại A,
;
Ta lại có: đồng dạng
Câu 23:
Cho tam giác ABC vuông tại A, I là một điểm trên cạnh AC. Đường tròn đường kính IC cắt BC ở E và cắt BI ở D.Chứng minh tứ giác ABCD nội tiếp được trong đường tròn
 Xem đáp án
Xem đáp án
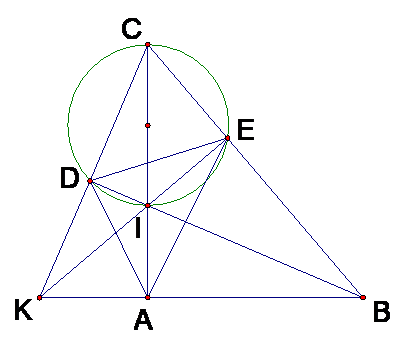
Chứng minh tứ giác ABCD nội tiếp được trong đường tròn.
Ta có
(góc nội tiếp chắn nửa đường tròn).
( tam giác vuông tại A).
Mặt khác hai đỉnh D,A cùng nhìn BC dưới một góc .
Vậy tứ giác ABCD nội tiếp được trong đường tròn.
Câu 24:
Cho tam giác vuông tại ABC, A,I là một điểm trên cạnh AC. Đường tròn đường kính IC cắt BC ở E và cắt BI ở D. Chứng minh DB là phân giác của góc ADE.
 Xem đáp án
Xem đáp án
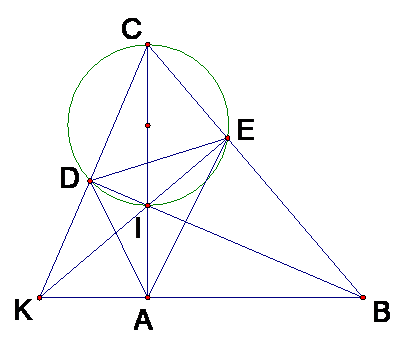
Chứng minh DB là phân giác của góc ADE.
Do tứ giác ABCD nội tiếp được trong đường tròn.
Nên (cùng chắn cung AB).
(cùng chắn cung IE của đường tròn đường kính IC).
.
Vậy DB là phân giác của góc ADE.
Câu 25:
Cho tam giác ABC vuông tại A,I là một điểm trên cạnh AC. Đường tròn đường kính IC cắt BC ở E và cắt BI ở D. Chứng minh I là tâm đường tròn nội tiếp tam giác ADE.
 Xem đáp án
Xem đáp án
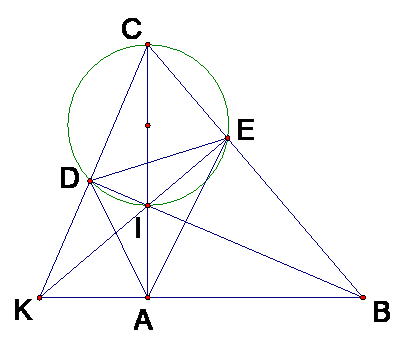
Chứng minh I là tâm đường tròn nội tiếp tam giác .
Chứng minh được tứ giác ANEI nội tiếp được trong đường tròn.
(cùng chắn cung IE).
Mặt khác vì tứ giác ABCD nội tiếp được trong đường tròn.
Nên (cùng chắn cung CD).
là phân giác của góc DAE.
Mà DB cắt AC tại I. Do đó I là tâm đường tròn nội tiếp tam giác .
Câu 26:
Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm M không trùng với A và C. Vẽ đường tròn đường kính MC, cắt cạnh BC tại D. Các đường thẳng BM và AD lần lượt cắt đường tròn tại các điểm E,F. Chứng minh rằng:. Suy ra
 Xem đáp án
Xem đáp án
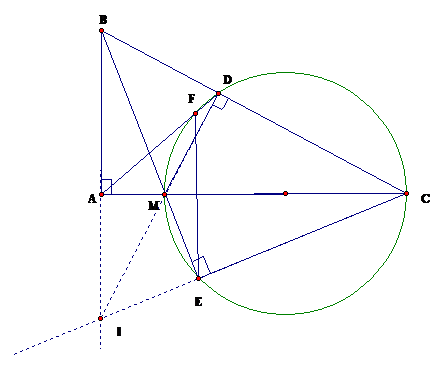
Vì và chung nên .
Do đó .
Câu 27:
Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm M không trùng với A và C. Vẽ đường tròn đường kính MC, cắt cạnh BC tại D. Các đường thẳng BM và AD lần lượt cắt đường tròn tại các điểm E,F. Chứng minh rằng: Các tứ giác ABDM và AECB nội tiếp
 Xem đáp án
Xem đáp án
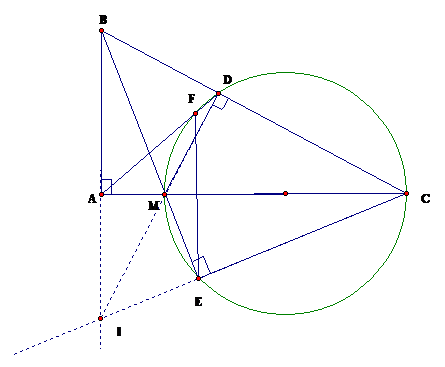
Vì nên tứ giác AMBD nội tiếp.
Vì nên tứ giác AECB nội tiếpCâu 28:
Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm M không trùng với A và C. Vẽ đường tròn đường kính MC, cắt cạnh BC tại M. Các đường thẳng BM và AD lần lượt cắt đường tròn tại các điểm E,F. Chứng minh rằng:
 Xem đáp án
Xem đáp án
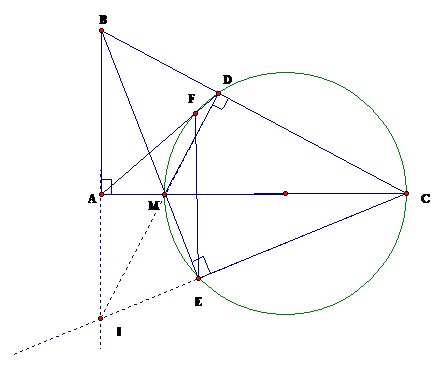
Ta có: ( cùng chắn )
( cùng chắn )
Suy ra .
Câu 29:
Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm M không trùng với A và C. Vẽ đường tròn đường kính MC, cắt cạnh BC tại M. Các đường thẳng BM và AD lần lượt cắt đường tròn tại các điểm E,F. Chứng minh rằng: Các đường thẳng đồng quy.
 Xem đáp án
Xem đáp án
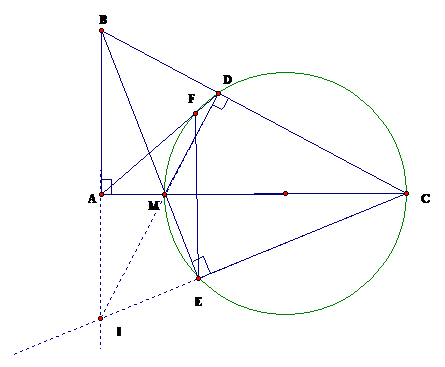
Giả sử AB cắt EC tại I. Ta có CA,BE là đường cao của tam giác BIC.
M là trực tâm của .
Mà thẳng hàng. Vậy đồng quy tại M.
Câu 30:
Hai đường tròn và tiếp xúc ngoài tại gọi AC và BC là hai đường kính đi qua C của đường tròn (O) và (O'). DE là dây cung của đường tròn (O) vuông góc với AB tại trung điểm M của AB. Tia DC cắt đường tròn (O') tại điểm thứ 2 là F. Tứ giác ADBE là hình gì? Vì sao?
 Xem đáp án
Xem đáp án
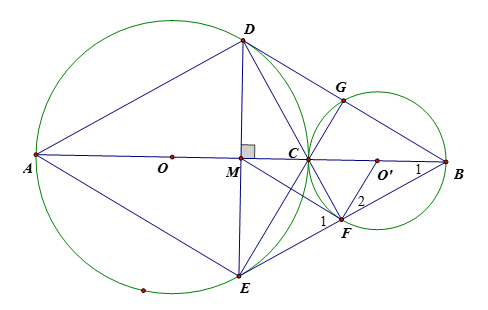
Câu 31:
Hai đường tròn và tiếp xúc ngoài tại gọi AC và BC là hai đường kính đi qua C của đường tròn (O) và (O'). DE là dây cung của đường tròn (O) vuông góc với AB tại trung điểm M của AB. Tia DC cắt đường tròn (O') tại điểm thứ 2 là F. Chứng minh ba điểm B, F, E thẳng hàng
 Xem đáp án
Xem đáp án
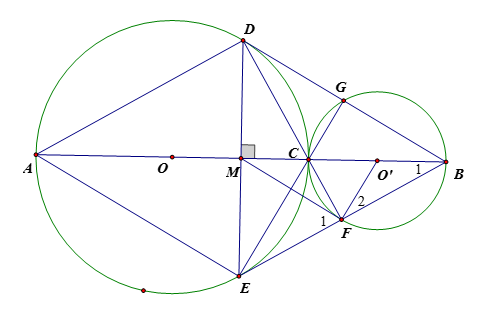
Câu 32:
Hai đường tròn và tiếp xúc ngoài tại gọi AC và BC là hai đường kính đi qua C của đường tròn (O) và (O'). DE là dây cung của đường tròn (O) vuông góc với AB tại trung điểm M của AB. Tia DC cắt đường tròn (O') tại điểm thứ 2 là F. DB cắt đường tròn (O') tại điểm thứ hai là G. Chứng minh DF, EG và AB đồng quy
 Xem đáp án
Xem đáp án
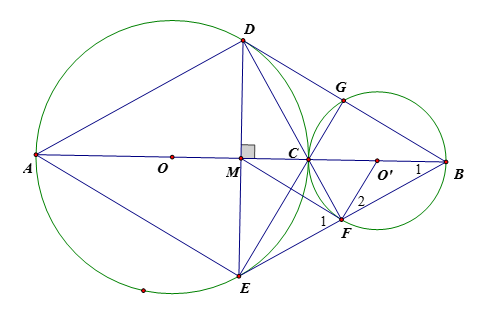
Câu 33:
Hai đường tròn (O;R) và (O';r) tiếp xúc ngoài tại gọi AC và BC là hai đường kính đi qua C của đường tròn (O) và (O'). DE là dây cung của đường tròn (O) vuông góc với AB tại trung điểm M của AB. Tia DC cắt đường tròn (O') tại điểm thứ 2 là F. Chứng minh MF là tiếp tuyến của (O')
 Xem đáp án
Xem đáp án
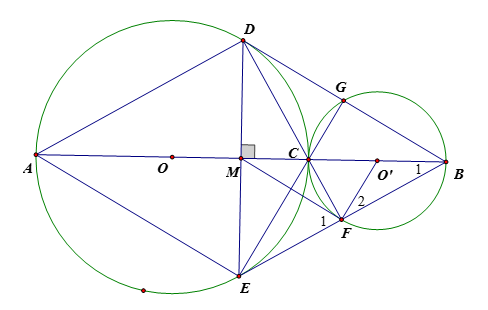
Nhận thấy và mà nên , suy ra . Vậy MF là tia tiếp tuyến của đường tròn tâm O’.
Câu 34:
Cho ∆ABC (AC > AB, ). Gọi I, K theo thứ tự là trung điểm của AB, AC. Các đường tròn đường kính AB, AC cắt nhau tại điểm thứ hai D; tia BA cắt đường tròn (K) tại điểmt hứ hai E; tia CA cắt đường tròn (I) tại điểm thứ hai F. Chứng minh tứ giác BFEC nội tiép
 Xem đáp án
Xem đáp án
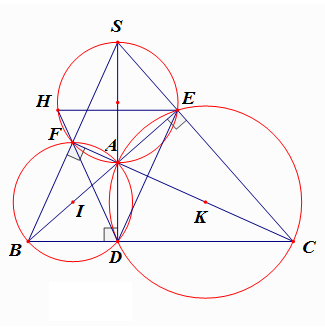
Áp dụng định lý góc nội tiếp
chắn nửa đường tròn, ta có:
; ;
suy ra . Khi đó E,F là hai đỉnh liên tiếp cùng nhìn BC dưới một góc bằng nhau.
Vậy tứ giác BFEC nội tiếp.
Câu 35:
Cho ∆ABC (AC > AB, ). Gọi I, K theo thứ tự là trung điểm của AB, AC. Các đường tròn đường kính AB, AC cắt nhau tại điểm thứ hai D; tia BA cắt đường tròn (K) tại điểmt hứ hai E; tia CA cắt đường tròn (I) tại điểm thứ hai F.Chứng minh ba đường thẳng AD, BF, CE đồng quy.
 Xem đáp án
Xem đáp án
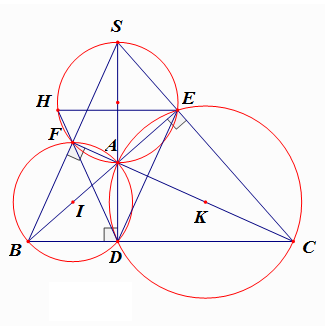
Câu 36:
Cho ∆ABC (AC > AB, ). Gọi I, K theo thứ tự là trung điểm của AB, AC. Các đường tròn đường kính AB, AC cắt nhau tại điểm thứ hai D; tia BA cắt đường tròn (K) tại điểmt hứ hai E; tia CA cắt đường tròn (I) tại điểm thứ hai F.Gọi H là giao điểm thứ hai của tia DF với đường tròn ngoại tiếp tam giác AEF, hãy so sánh DH và DE.
 Xem đáp án
Xem đáp án
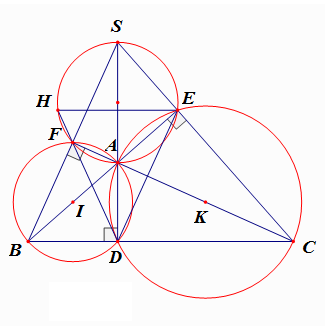
Ta có AEHF nội tiếp nên mặt khác . (1)
Vận dụng góc nội tiếp, tứ giác nội tiếp ta có:
DA là đường phân giác (2)
Từ (1) và (2) suy ra DEH cân tại D suy ra .
Câu 37:
Cho tam giác ABC vuông tại A và một điểm D nằm giữa A và B. Đường tròn (O) đường kính BD cắt BC tại E. Các đường thẳng CD, AE lần lượt cắt đường tròn (O) tại các điểm thứ hai là F, G. Chứng minh rằng :Các tứ giác ADEC và AFBC nội tiếp
 Xem đáp án
Xem đáp án
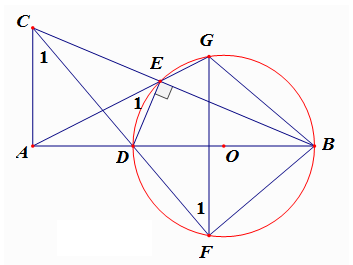
tứ giác ADEC nội tiếp.
tứ giác AFBC nội tiếp.
Câu 38:
Cho tam giác ABC vuông tại A và một điểm D nằm giữa A và B. Đường tròn (O) đường kính BD cắt BC tại E. Các đường thẳng CD, AE lần lượt cắt đường tròn (O) tại các điểm thứ hai là F, G. Chứng minh rằng :AD.AB = AG.AE
 Xem đáp án
Xem đáp án
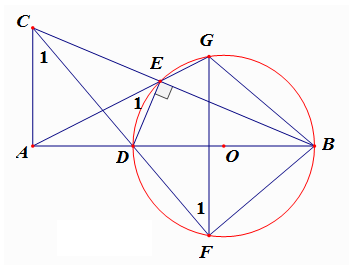
Ta có
Câu 39:
Cho tam giác ABC vuông tại A và một điểm D nằm giữa A và B. Đường tròn (O) đường kính BD cắt BC tại E. Các đường thẳng CD, AE lần lượt cắt đường tròn (O) tại các điểm thứ hai là F, G. Chứng minh rằng :AC//FG
 Xem đáp án
Xem đáp án
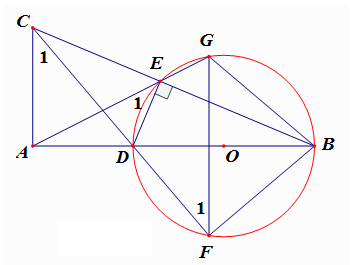
Tứ giác ACED nội tiếp .
Tứ giác DFGE nội tiếp .
Suy ra .