Cho hình vuông ABCD cạnh a .Vẽ cung BD tâm A bán kính a (nằm trong hình vuông ) .một tiếp tuyến bất kỳ với cung đó cắt BC, CD theo thứ tự ở M và N. Tính độ dài nhỏ nhất của MN.
Giải bởi Vietjack
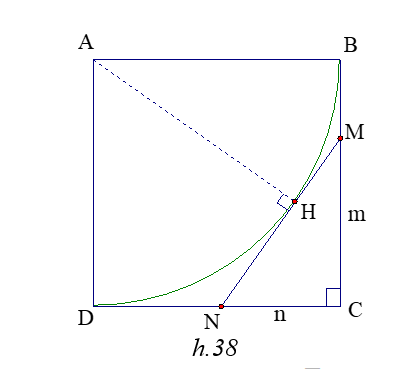
Đặt CM = m , CN = n , MN = x
m + n + x = 2CD = 2a và m2 +n2 = x2
Do đó : x2= m2 +n2 ≥
2x2 ≥ ( 2a - x)2 Þ ≥ 2a - x
x ≥
min MN =2a Û m = n . Khi đó tiếp tuyến MN // BD , AM là tia phân giác của
AN là phân giác của
Cho DABC vuông cân tại A các điểm D,E theo thứ tự di chuyển trên các cạnh AB , AC sao cho BD = AE . Xác định vị trí các điểm D,E sao cho :Tứ giác BDEC có diện tích lớn nhất
Cho DABC vuông cân tại A các điểm D,E theo thứ tự di chuyển trên các cạnh AB , AC sao cho BD = AE . Xác định vị trí các điểm D,E sao cho :DE có độ dài nhỏ nhất .
Cho D ABC vuông tại A có BC = a , diện tích là S . Gọi m là trung điểm của BC . Hai dường thẳng thay đổi qua M và vuông góc với nhau cắt các cạnh AB , AC ở D ,E .Tìm :Giá trị nhỏ nhất của đoạn thẳng DE .
Cho điểm m di chuyển trên đoạn thẳng AB .Vẽ các tam giác đềuAMC và BMD về một phía của AB . Xác định vị trí của M để tổng diện tích hai tam giác đều tren là nhỏ nhất .
Cho đường tròn (O;R) đường kính BC , A là một điểm di động trên đường tròn . Vẽ tam giác đều ABM có A và M nằm cùng phía đối với BC . Gọi H là chân đường vuông góc kẻ từ C xuống MB. Gọi D, E , F, G theo thứ tự là trung điểm của OC, CM, MH, OH . Xác định vị trí của điểm A để diện tích tứ giác DEFG đạt giá trị lớn nhất.
Cho đoạn thẳng AB và một điểm C trên AB .Vẽ trên cùng một nửa mặt phẳng bờ AB các nửa đường tròn có đường kính AB,AC,BC . Xác định vị trí của điểm C trên đoạn AB để diện tích phần giới hạn bởi ba nửa đường tròn đó dạt giá trị lớn nhất.
Cho nửa đường tròn có đường kính AB = 10 cm .Một dây CD có độ dài 6cm có hai đầu di chuyển trên nửa đường tròn . Gọi E và F theo thứ tự là hình chiếu của A và B trên CD. Tính diện tích lớn nhất của tứ giác ABFE.
Cho DABC nội tiếp đường tròn (O) D là điểm bất kỳ thuộc cung BC không chứa A và không trùng với B,C. Gọi H,I,K theo thứ tự là chân các đường vuông góc kẻ từ D đến các đường thẳng BC , AC, AB . Đặt BC = a , AC = b ,AB = c, DH = x , DI = y , DK = z . Chứng minh rằng :
Cho hình vuông ABCD . Hãy xác định đường thẳng d đi qua tâm hình vuông sao cho tổng các khoảng cách từ bốn đỉnh của hình vuông đến đường thẳng đó là : Lớn nhất
Cho DABC nội tiếp đường tròn (O) D là điểm bất kỳ thuộc cung BC không chứa A và không trùng với B,C. Gọi H,I,K theo thứ tự là chân các đường vuông góc kẻ từ D đến các đường thẳng BC , AC, AB . Đặt BC = a , AC = b ,AB = c, DH = x , DI = y , DK = z .Tìm vị trí của điểm D để tổng nhỏ nhất
Cho hình vuông ABCD . Hãy xác định đường thẳng d đi qua tâm hình vuông sao cho tổng các khoảng cách từ bốn đỉnh của hình vuông đến đường thẳng đó là :Nhỏ nhất
