Trong mặt phẳng tọa độ Oxy, cho A(2; –3), B(4; 7). Tọa độ trung điểm I của đoạn thẳng AB là:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Gọi I(xI; yI). Suy ra \(\overrightarrow {AI} = \left( {{x_I} - 2;{y_I} + 3} \right)\) và \(\overrightarrow {IB} = \left( {4 - {x_I};7 - {y_I}} \right)\).
Ta có I là trung điểm của đoạn thẳng AB.
\( \Leftrightarrow \overrightarrow {AI} = \overrightarrow {IB} \)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_I} - 2 = 4 - {x_I}\\{y_I} + 3 = 7 - {y_I}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}2{x_I} = 6\\2{y_I} = 4\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_I} = 3\\{y_I} = 2\end{array} \right.\)
Suy ra tọa độ I(3; 2).
Vậy ta chọn phương án A.
Cho điểm A(–2; 3) và \(\overrightarrow {AM} = 3\vec i - 2\vec j\).
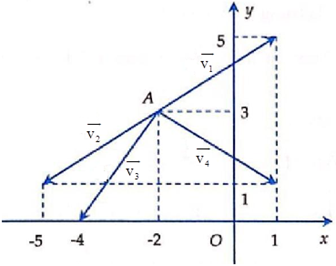
Vectơ nào trong hình là \(\overrightarrow {AM} \)?
Trong mặt phẳng tọa độ Oxy, cho hai điểm B(–1; 3) và C(5; 2). Tọa độ của \(\overrightarrow {BC} \) là:
Trong mặt phẳng tọa độ Oxy, cho các điểm M(0; – 2), N(2; 4), P(– 5; 1), Q(– 3; 7). Cặp vectơ nào sau đây bằng nhau?
Trong mặt phẳng tọa độ Oxy, cho ba điểm E (2; – 3), F(4; 7), G(1; 5). Nếu \(\overrightarrow {EF} = \overrightarrow {GH} \) thì tọa độ điểm H là:
Trong mặt phẳng tọa độ Oxy, cho \[\vec a = \left( {1;5} \right)\] và \(\vec b = \left( {3u + v;u - 2v} \right)\). Khi đó \(\vec a = \vec b\) khi và chỉ khi:
Trong mặt phẳng tọa độ Oxy, cho \[\vec g = \left( {2x;1 - 3y} \right)\] và \[\vec h = \left( {x - y;3y - x} \right)\]. Khi đó \(\vec g = \vec h\) khi và chỉ khi: