Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a . Gọi I và J lần lượt là trung điểm của SC và BC . Số đo của góc (IJ, CD) bằng
Giải bởi Vietjack
Chọn C.
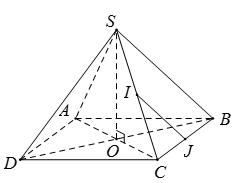
Gọi O là tâm của hình vuông ABCD => O là tâm đường tròn ngoại tiếp của hình vuông ABCD (1).
Ta có: SA = SB = SC = SD => S nằm trên trục của đường tròn ngoại tiếp hình vuông ABCD (2).
Từ (1) và (2)
Từ giả thiết ta có: IJ // SB (do IJ là đường trung bình của ).
Mặt khác, ta lại có đều, do đó
Cho tứ diện ABCD có ( I, J lần lượt là trung điểm của BC và AD ). Số đo góc giữa hai đường thẳng AB và CD là :
Cho tứ diện đều ABCD (Tứ diện có tất cả các cạnh bằng nhau). Số đo góc giữa hai đường thẳng AB và CD bằng
Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD bằng:
độ cao của lần rơi trước. Giả sử quả bóng luôn chuyển động vuông góc với mặt đất. Tổng quãng đường bóng đã di chuyển (từ lúc bắt đầu thả đến lúc bóng không di chuyển nữa) gần nhất với kết quả nào sau đây?
. Tính tổng 
, trong đó a là tham số thực. Tìm a để 
bằng:
là:
là:
bằng
bằng