55 câu hỏi trắc nghiệm thuộc Dạng 1: Tính góc giữa hai đường thẳng có đáp án

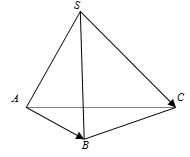
Câu 1:

Cho tứ diện ABCD có $A B = C D = a, I J = \frac{a \sqrt{3}}{2}$ ( I, J lần lượt là trung điểm của BC và AD). Số đo góc giữa hai đường thẳng AB và CD là:

A. $30^{O}$

B. $45^{O}$

C. $60^{O}$

D. $90^{O}$

Xem đáp án

Chọn C.

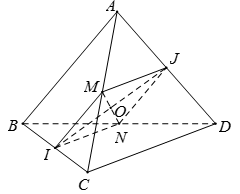
Cho tứ diện ABCD có AB = CD = a, IJ = a căn bậc hai 3/2 ( I, J lần lượt là trung điểm của BC và AD). Số đo góc giữa hai đường thẳng AB và CD là: (ảnh 1)

Gọi M, N lần lượt là trung điểm AC, BC.

Ta có:

$\{\begin{cases} M I = N I = \frac{1}{2} A B = \frac{1}{2} C D = \frac{a}{2} \\ M I // A B // C D // N I \end{cases} \Rightarrow M I N J$ là hình thoi.

Gọi O là giao điểm của MN và IJ.

Ta có: $\hat{M I N} = 2 \hat{M I O}$

Xét tam giác MIO vuông tại O, ta có: $\cos \hat{M I O} = \frac{I O}{M I} = \frac{\frac{a \sqrt{3}}{4}}{\frac{a}{2}} = \frac{\sqrt{3}}{2} \Rightarrow \hat{M I O} = 30 ° \Rightarrow \hat{M I N} = 60 °$

Mà: $(A B, C D) = (I M, I N) = \hat{M I N} = 60 °$

Câu 2:

Cho hình hộp ABCD.A'B'C'D' . Giả sử tam giác AB'C và A'DC' đều có 3 góc nhọn. Góc giữa hai đường thẳng AC và A'D là góc nào sau đây?

A. $\hat{B D B^{'}}$

B. $\hat{A B^{'} C}$

C. $\hat{D B^{'} B}$

D. $\hat{D A^{'} C^{'}}$

Xem đáp án

Chọn D.

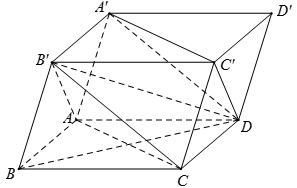
Cho hình hộp ABCD.A'B'C'D' . Giả sử tam giác AB'C và A'DC' đều có 3 góc nhọn. Góc giữa hai đường thẳng AC và A'D là góc nào sau đây? (ảnh 1)

Ta có: AC // A'C' (tính chất của hình hộp)

$\Rightarrow (A C, A^{'} D) = (A^{'} C^{'}, A^{'} D) = \hat{D A^{'} C^{'}}$ (do giả thiết cho tam giác DA'C' nhọn).

Câu 3:

Cho tứ diện đều ABCD (Tứ diện có tất cả các cạnh bằng nhau). Số đo góc giữa hai đường thẳng AB và CD bằng

A. $30^{o}$

B. $45^{o}$

C. $60^{o}$

D. $90^{o}$

Xem đáp án

Chọn D.

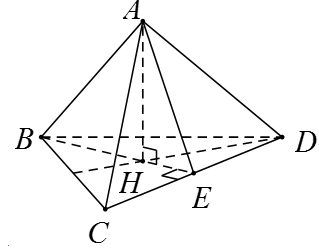
Cho tứ diện đều ABCD (Tứ diện có tất cả các cạnh bằng nhau). Số đo góc giữa hai đường thẳng AB và CD bằng (ảnh 1)

Gọi H là tâm đường tròn ngoại tiếp $Δ B C D \Rightarrow A H ⊥ (B C D)$

Gọi E là trung điểm CD $\Rightarrow B E ⊥ C D$ (do tam giác BCD đều).

Do $A H ⊥ (B C D) \Rightarrow A H ⊥ C D$

Ta có: $\{\begin{cases} C D ⊥ B E \\ C D ⊥ A H \end{cases} \Rightarrow C D ⊥ (A B E) \Rightarrow C D ⊥ A B \Rightarrow \hat{(A B, C D)} = 90 °$

Câu 4:

Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a . Gọi M và N lần lượt là trung điểm của AD và SD . Số đo của góc (MN, SC) bằng

A. 30°

B. 45°

C. 60°

D. 90°

Xem đáp án

Chọn D.

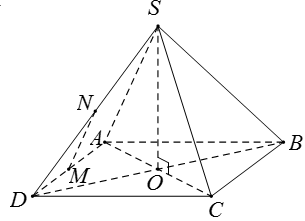
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a . Gọi M và N lần lượt là trung điểm của AD và SD . (ảnh 1)

Gọi O là tâm của hình vuông ABCD => O là tâm đường tròn ngoại tiếp của hình vuông ABCD (1).

Ta có: SA = SB = SC = SD => S nằm trên trục của đường tròn ngoại tiếp hình vuông ABCD (2).

Từ (1) và (2) $\Rightarrow S O ⊥ (A B C D)$

Từ giả thiết ta có: MN // SA (do MN là đường trung bình của $Δ S A D$ ). $\Rightarrow (M N, S C) = (S A, S C)$

Xét $Δ S A C$ , ta có: $\{\begin{cases} S A^{2} + S C^{2} = a^{2} + a^{2} = 2 a^{2} \\ A C^{2} = 2 A D = 2 a^{2} \end{cases} \Rightarrow Δ S A C$ vuông tại S. $\Rightarrow S A ⊥ S C$

$\Rightarrow (S A, S C) = (M N, S C) = 90 °$

.

Câu 5:

Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a . Gọi I và J lần lượt là trung điểm của SC và BC . Số đo của góc (IJ, CD) bằng

A. 30°

B. 45°

C. 60°

D. 90°

Xem đáp án

Chọn C.

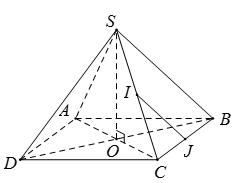
Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a . Gọi I và J lần lượt là trung điểm của SC và BC . Số đo của góc (IJ, CD) bằng (ảnh 1)

Gọi O là tâm của hình vuông ABCD => O là tâm đường tròn ngoại tiếp của hình vuông ABCD (1).

Ta có: SA = SB = SC = SD => S nằm trên trục của đường tròn ngoại tiếp hình vuông ABCD (2).

Từ (1) và (2) $\Rightarrow S O ⊥ (A B C D)$

Từ giả thiết ta có: IJ // SB (do IJ là đường trung bình của $Δ S A B$ ). $\Rightarrow (I J, C D) = (S B, A B)$

Mặt khác, ta lại có $Δ S A B$ đều, do đó $\hat{S B A} = 60 ° \Rightarrow (S B, A B) = 60 ° \Rightarrow (I J, C D) = 60 °$

Câu 6:

Cho tứ diện ABCD có AB = CD. Gọi I, J, E, F lần lượt là trung điểm của AC, BC, BD, AD. Góc giữa (IE, JF) bằng

A. 30°

B. 45°

C. 60°

D. 90°

Xem đáp án

Chọn D.

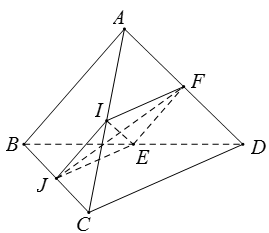
Cho tứ diện ABCD có AB = CD. Gọi I, J, E, F lần lượt là trung điểm của AC, BC, BD, AD. Góc giữa (IE, JF) bằng (ảnh 1)

Từ giả thiết ta có: $\{\begin{cases} I J // E F // A B \\ J E // I F // C D \end{cases}$ (tính chất đường trung bình trong tam giác)

Từ đó suy ra tứ giác IJEF là hình bình hành.

Mặt khác: $A B = C D \Rightarrow I J = \frac{1}{2} A B = J E = \frac{1}{2} C D \Rightarrow A B C D$ là hình thoi $\Rightarrow I E ⊥ J F$ (tính chất hai đường chéo của hình thoi)

$\Rightarrow (I E, J F) = 90 °$ .

Câu 7:

Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ $\vec{A B}$ và $\vec{D H}$ ?

A. 45°

B. 90°

C. 120°

D. 60°

Xem đáp án

Chọn B.

$\begin{array}{l} A B ⊥ A E \\ A E // D H \end{array}\} \Rightarrow A B ⊥ D H \Rightarrow \hat{(A B, D H)} = 90 °$

Câu 8:

Trong không gian cho hai hình vuông ABCD và ABC'D' có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm O và O'. Hãy xác định góc giữa cặp vectơ

\vec{A B}

và

\vec{O O'}

?

A. 60°

B. 45°

C. 120°

D. 90°

Xem đáp án

Chọn D.

Vì ABCD và A'B'C'D' là hình vuông nên $A D // B C'; A D = B C' \Rightarrow A D B C'$ là hình bình hành

Mà O; O' là tâm của 2 hình vuông nên O; O' là trung điểm của BD và AC' => OO' là đường trung bình của ADBC' => OO' // AD

Mặt khác, $A D ⊥ A B$ nên $O O' ⊥ A B ⊥ \Rightarrow \hat{(O O', A B)} = 90^{o}$

Câu 9:

Cho tứ diện ABCD có AB = AC = AD và

\hat{B A C} = \hat{B A D} = 60^{0}, \hat{C A D} = 90^{0}

. Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ

\vec{I J}

và

\vec{C D}

?

A. 45°

B. 90°

C. 60°

D. 120°

Xem đáp án

Chọn B.

Ta có BAC và BAD là 2 tam giác đều, I là trung điểm của AB nên CI = DI (2 đường trung tuyến của 2 tam giác đều chung cạnh AB ) nên CID là tam giác cân ở I . Do đó $I J ⊥ C D .$

Câu 10:

Cho hình chóp S.ABC có SA = SB = SC và

\hat{A S B} = \hat{B S C} = \hat{C S A}

. Hãy xác định góc giữa cặp vectơ

\vec{S B}

và

\vec{A C}

?

A. 60°

B. 120°

C. 45°

D. 90°

Xem đáp án

Chọn D.

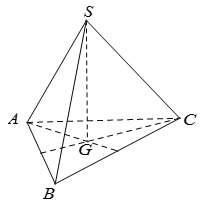
Cho hình chóp S.ABC có SA = SB = SC và góc ASB = góc BSC = góc CSA. Hãy xác định góc giữa cặp vectơ SB và góc AC? (ảnh 1)

Ta có: $Δ S A B = Δ S B C = Δ S C A (c - g - c)$

$\Rightarrow A B = B C = C A$

Do đó tam giác ABC đều. Gọi G là trọng tâm của tam giác ABC.

Vì hình chóp S.ABC có SA = SB = SC nên hình chiếu của S trùng với G

Hay $S G ⊥ (A B C)$ .

Ta có: $\{\begin{cases} A C ⊥ B G \\ A C ⊥ S G \end{cases} \Rightarrow A C ⊥ (S B G)$

Suy ra $A C ⊥ S B$

Vậy góc giữa cặp vectơ $\vec{S B}$ và $\vec{A C}$ bằng $90^{0}$

Câu 11:

Cho tứ diện ABCD có AB = AC = AD và $\hat{B A C} = \hat{B A D} = 60^{0}, \hat{C A D} = 90^{0}$ . Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ $\vec{A B}$ và $\vec{I J}$ ?

A. 120°

B. 90°

C. 60°

D. 45°

Xem đáp án

Chọn B.

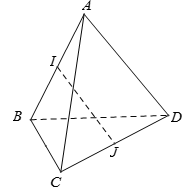
Cho tứ diện ABCD có AB = AC = AD và góc BAC = góc BAD = 60 độ, góc CAD = 90 độ. Gọi I và J lần lượt là trung điểm của AB và CD. (ảnh 1)

Xét tam giác ICD có J là trung điểm đoạn CD .

Ta có: $\vec{I J} = \frac{1}{2} (\vec{I C} + \vec{I D})$

Vì tam giác ABC có AB = AC và $\hat{B A C} = 60 °$

Nên tam giác ABC đều. Suy ra: $C I ⊥ A B$

Tương tự ta có tam giác ABD đều nên $D I ⊥ A B$

Xét $\vec{I J} . \vec{A B} = \frac{1}{2} (\vec{I C} + \vec{I D}) . \vec{A B} = \frac{1}{2} \vec{I C} . \vec{A B} + \frac{1}{2} \vec{I D} . \vec{A B} = \vec{0}$

Câu 12:

Cho tứ diện ABCD có trọng tâm G. Chọn khẳng định đúng?

A. $A B^{2} + A C^{2} + A D^{2} + B C^{2} + B D^{2} + C D^{2} = 3 (G A^{2} + G B^{2} + G C^{2} + G D^{2})$

B. $A B^{2} + A C^{2} + A D^{2} + B C^{2} + B D^{2} + C D^{2} = 4 (G A^{2} + G B^{2} + G C^{2} + G D^{2})$

C. $A B^{2} + A C^{2} + A D^{2} + B C^{2} + B D^{2} + C D^{2} = 6 (G A^{2} + G B^{2} + G C^{2} + G D^{2})$

D. $A B^{2} + A C^{2} + A D^{2} + B C^{2} + B D^{2} + C D^{2} = 2 (G A^{2} + G B^{2} + G C^{2} + G D^{2})$

Xem đáp án

Chọn B.

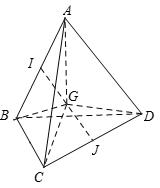
Cho tứ diện ABCD có trọng tâm G . Chọn khẳng định đúng? A. AB^2 + AC^2 + AD^2 + BC^2 + BD^2 + CD^2 = 3(GA^2 + GB^2 + GC^2 + GD^2) (ảnh 1)

$\begin{array}{l} A B^{2} + A C^{2} + A D^{2} + B C^{2} + B D^{2} + C D^{2} \\ = {(\vec{A G} + \vec{G B})}^{2} + {(\vec{A G} + \vec{G C})}^{2} + {(\vec{A G} + \vec{G D})}^{2} + {(\vec{B G} + \vec{G C})}^{2} + {(\vec{B G} + \vec{G D})}^{2} + {(\vec{C G} + \vec{G D})}^{2} \\ = 3 A G^{2} + 3 B G^{2} + 3 C G^{2} + 3 D G^{2} + 2 (\vec{A G} . \vec{G B} + \vec{A G} . \vec{G C} + \vec{A G} . \vec{G D} + \vec{B G} . \vec{G D} + \vec{B G} . \vec{G D} + \vec{C G} . \vec{G D}) (1) \end{array}$

Lại có:

$\begin{array}{l} (\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D}) = \vec{0} \\ \Leftrightarrow G A^{2} + G B^{2} + G C^{2} + G D^{2} \\ = 2 (\vec{A G} . \vec{G B} + \vec{A G} . \vec{G C} + \vec{A G} . \vec{G D} + \vec{B G} . \vec{G D} + \vec{B G} . \vec{G D} + \vec{C G} . \vec{G D}) (2) \end{array}$

Từ (1) và (2) ta có điều phải chứng minh.

Câu 13:

Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Góc giữa AB và CD là?

A. 120°

B. 60°

C. 90°

D. 30°

Xem đáp án

Chọn C.

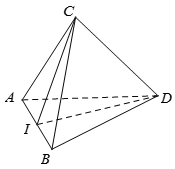
Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Góc giữa AB và CD là? (ảnh 1)

Gọi I là trung điểm của AB

Vì ABC và ABD là các tam giác đều

Nên $\{\begin{cases} C I ⊥ A B \\ D I ⊥ A B \end{cases}$

Suy ra $A B ⊥ (C I D) \Rightarrow A B ⊥ C D$

Câu 14:

Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC . Số đo của góc (IJ, CD) bằng:

A. 90°

B. 45°

C. 30°

D. 60°

Xem đáp án

Chọn D.

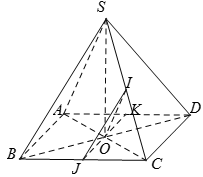
Gọi O là tâm của hình thoi ABCD .

Ta có: OJ // CD

Nên góc giữa IJ và CD bằng góc giữa IJ và OJ.

Xét tam giác IOJ có

$I J = \frac{1}{2} S B = \frac{a}{2}, O J = \frac{1}{2} C D = \frac{a}{2}, I O = \frac{1}{2} S A = \frac{a}{2}$

Nên tam giác IOJ đều.

Vậy góc giữa IJ và CD bằng góc giữa IJ và OJ bằng góc .

Câu 15:

Cho hình hộp ABCD.A'B'C'D'. Giả sử tam giác AB'C và A'DC' đều có 3 góc nhọn. Góc giữa hai đường thẳng AC và A'D là góc nào sau đây?

A. $\hat{A B^{'} C}$

B. $\hat{D A^{'} C^{'}}$

C. $\hat{B B^{'} D}$

D. $\hat{B D B^{'}}$

Xem đáp án

Chọn B.

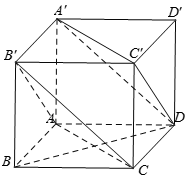
Ta có: AC // A'C' nên góc giữa hai đường thẳng AC và A'D là góc giữa hai đường thẳng A'C' và A'D bằng góc nhọn $\hat{D A^{'} C^{'}}$ (Vì tam giác A'DC' đều có 3 góc nhọn)

Câu 16:

Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD bằng:

A. 60°

B. 30°

C. 90°

D. 60°

Xem đáp án

Chọn C.

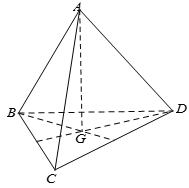
Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD bằng: A. 60 độ B. 30 độ C. 90 độ D. 45 độ (ảnh 1)

Gọi G là trọng tâm tam giác ABC.

Vì tứ diện ABCD đều nên $A G ⊥ (B C D)$ .

Ta có: $\{\begin{cases} C D ⊥ A G \\ C D ⊥ B G \end{cases} \Rightarrow C D ⊥ (A B G) \Rightarrow C D ⊥ A B$ .

Vậy số đo góc giữa hai đường thẳng AB và CD bằng $90^{0}$

Câu 17:

Cho tứ diện ABCD có hai cặp cạnh đối vuông góc. Cắt tứ diện đó bằng một mặt phẳng song song với một cặp cạnh đối diện của tứ diện. Trong các mệnh đề sau mệnh đề nào đúng?

A. Thiết diện là hình chữ nhật.

B. Thiết diện là hình vuông.

C. Thiết diện là hình bình hành.

D. Thiết diện là hình thang.

Xem đáp án

Chọn A.

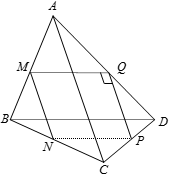
Cho tứ diện ABCD có hai cặp cạnh đối vuông góc. Cắt tứ diện đó bằng một mặt phẳng song song với một cặp cạnh đối diện của tứ diện. (ảnh 1)

Gỉa sử thiết diện là tứ giác MNPQ.

Ta có: MN // PQ và MN = PQ nên MNPQ là hình bình hành

Lại có $A C ⊥ B D \Rightarrow M Q ⊥ P Q$

Vậy tứ giác MNPQ là hình chữ nhật.

Câu 18:

Cho tứ diện ABCD . Chứng minh rằng nếu $\vec{A B} . \vec{A C} = . \vec{A C} . \vec{A D} = \vec{A D} . \vec{A B}$ thì $A B ⊥ C D, A C ⊥ B D, A D ⊥ B C$ . Điều ngược lại đúng không?

Sau đây là lời giải:

Bước 1: $\vec{A B} . \vec{A C} = . \vec{A C} . \vec{A D} \Leftrightarrow \vec{A C} . (\vec{A B} - \vec{A D}) = 0 \Leftrightarrow A C ⊥ B D$

Bước 2 Chứng minh tương tự, từ $\vec{A C} . \vec{A D} = \vec{A D} . \vec{A B}$ ta được $A D ⊥ B C$ và $\vec{A B} . \vec{A C} = \vec{A D} . \vec{A B}$ ta được $A B ⊥ C D$

Bước 3: Ngược lại đúng, vì quá trình chứng minh ở bước 1 và 2 là quá trình biến đổi tương đương.

Bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?

A. Sai ở bước 3.

B. Đúng

C. Sai ở bước 2.

D. Sai ở bước 1.

Xem đáp án

Chọn B.

Bài giải đúng.

Câu 19:

Cho hình chóp ABCD có SA = SB = SC và

\hat{A S B} = \hat{B S C} = \hat{C S A}

. Hãy xác định góc giữa cặp vectơ

\vec{S C}

và

\vec{A B}

?

A. 30°

B. 45°

C. 60°

D. 90°

Xem đáp án

Chọn D.

Cho hình chóp ABCD có SA = SB = SC và góc ASB = góc BSC = góc CSA. Hãy xác định góc giữa cặp vectơ SC và vecto AB ? (ảnh 1)

Ta có: $\vec{S C} . \vec{A B} = \vec{S C} . (\vec{S B} - \vec{S A}) = \vec{S C} . \vec{S B} - \vec{S C} . \vec{S A}$

$= S A . S B \cos \hat{B S C} - S C . S A . \cos \hat{A S C} = 0$

Vì $S A = S B = S C$ và $\hat{B S C} = \hat{A S C}$

Do đó: $(\vec{S C}, \vec{A B}) = 90^{0}$

Câu 20:

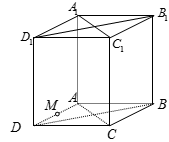
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo của góc (MN, SC) bằng:

A. 45°

B. 30°

C. 90°

D. 60°

Xem đáp án

Chọn C.

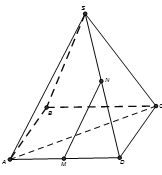
Ta có: $A C = a \sqrt{2}$

$\Rightarrow A C^{2} = 2 a^{2} = S A^{2} + S C^{2}$

$\Rightarrow Δ S A C$ vuông tại S.

Khi đó: $\vec{N M} . \vec{S C} = \frac{1}{2} \vec{S A} . \vec{S C} = 0 \Leftrightarrow (\vec{N M}, \vec{S C}) = 90 °$

$\Rightarrow (M N, S C) = 90 °$

Câu 21:

Cho hình lập phương $A B C D . A_{1} B_{1} C_{1} D_{1}$ . Chọn khẳng định sai?

A. Góc giữa AC và B₁D₁ bằng 90^o.

B. Góc giữa B₁D₁ và AA₁ bằng 60^o.

C. Góc giữa AD và B₁C bằng 45^o.

D. Góc giữa BD và A₁C₁ bằng 90^o.

Xem đáp án

Chọn B.

Cho hình lập phương ABCD.A1B1C1D1 . Chọn khẳng định sai? A. Góc giữa AC và B1D1 bằng 90 độ. (ảnh 1)

Ta có: $\vec{A A_{1}} . \vec{B_{1} D_{1}} = \vec{B B_{1}} . \vec{B D} = \vec{B B_{1}} . (\vec{B A} + \vec{B C})$

$= \vec{B B_{1}} . \vec{B A} + \vec{B B_{1}} . \vec{B C} = 0$

(vì $(\vec{B B_{1}}, \vec{B A}) = 90^{0}$ và $(\vec{B B_{1}}, \vec{B C}) = 90^{0}$ )

Do đó: $(\vec{A A_{1}}, \vec{B_{1} D_{1}}) = 90^{0} \Rightarrow (A A_{1}, B_{1} D_{1}) = 90^{0}$

Câu 22:

Cho hình lập phương $A B C D . A_{1} B_{1} C_{1} D_{1}$ có cạnh a. Gọi M là trung điểm $\vec{B_{1} M} . \vec{B D_{1}}$ . Giá trị là:

A. $\frac{1}{2} a^{2}$

B. $a^{2}$

C. $\frac{3}{4} a^{2}$

D. $\frac{3}{2} a^{2}$

Xem đáp án

Chọn A.

Cho hình lập phương ABCD.A1B1C1D1 có cạnh a . Gọi M là trung điểm AD . Giá trị vecto B1M. vecto BD1 là: (ảnh 1)

Ta có:

$\vec{B_{1} M} . \vec{B D_{1}} = (\vec{B_{1} B} + \vec{B A} + \vec{A M}) (\vec{B A} + \vec{A D} + \vec{D D_{1}}) \begin{array}{l} = \vec{B_{1} B} . \vec{D D_{1}} + {\vec{B A}}^{2} + \vec{A M} . \vec{A D} \\ = - a^{2} + a^{2} + \frac{a^{2}}{2} \\ = \frac{a^{2}}{2} \end{array}$

Câu 23:

Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau, mệnh đề nào có thể sai?

A. $A^{'} C^{'} ⊥ B D$

B. $B B^{'} ⊥ B D$

C. $A^{'} B ⊥ D C^{'}$

D. $B C^{'} ⊥ A^{'} D$

Xem đáp án

Chọn B.

Ta có: $\vec{B B^{'}} . \vec{B D} = \vec{B B^{'}} . (\vec{B A} + \vec{B C}) = \vec{B B^{'}} . \vec{B A} + \vec{B B^{'}} . \vec{B C}$

$= B B^{'} . B A (c o s \hat{B^{'} B A} + c o s \hat{B^{'} B C})$

Vì AA'B'B và ABCD là hai hình thoi bằng nhau nên

+ $\hat{B^{'} B A} = \hat{B^{'} B C} \Rightarrow \vec{B B^{'}} . \vec{B D} \neq 0$ suy ra BB' không vuông góc với BD

+ $\hat{B^{'} B A} + \hat{B^{'} B C} = 180^{0} \Rightarrow c o s \hat{B^{'} B A} = - c o s \hat{B^{'} B C} \Rightarrow \vec{B B^{'}} . \vec{B D} = 0$ suy ra $B B^{'} ⊥ B D$

Nên đáp án B có thể sai vì chưa có điều kiện của góc $\hat{B^{'} B A}$ và $\hat{B^{'} B C}$

Câu 24:

Cho hình lập phương ACBD.EFGH. Hãy xác định góc giữa cặp vectơ

\vec{A B}

và

\vec{E G}

?

A. 90°

B. 60°

C. 45°

D. 120°

Xem đáp án

Chọn C.

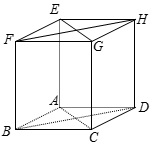
Cho hình lập phương ABCD.EFGH . Hãy xác định góc giữa cặp vectơ AB và vecto EG? (ảnh 1)

Ta có: EG // AC (do ACGE là hình chữ nhật)

$\Rightarrow (\vec{A B}, \vec{E G}) = (\vec{A B}, \vec{A C}) = \hat{B A C} = 45 °$

Câu 25:

Cho tứ diện ABCD đều cạnh bằng a. Gọi M là trung điểm CD, $α$ là góc giữa AC và BM. Chọn khẳng định đúng?

A. $c o s α = \frac{\sqrt{3}}{4}$

B. $c o s α = \frac{1}{\sqrt{3}}$

C. $c o s α = \frac{\sqrt{3}}{6}$

D. $α = 60 °$

Xem đáp án

Chọn C.

Cho tứ diện ABCD đều cạnh bằng a. Gọi M là trung điểm CD, là góc giữa AC và BM. Chọn khẳng định đúng? (ảnh 1)

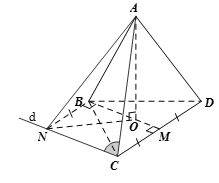
Gọi O là trọng tâm của $Δ B C D \Rightarrow A O ⊥ (B C D)$

Trên đường thẳng d qua C và song song BM lấy điểm N sao cho BMCN là hình chữ nhật, từ đó suy ra: $(\hat{A C, B M}) = (\hat{A C, C N}) = (\hat{A C N}) = α$

Có: $C N = B M = \frac{\sqrt{3}}{2} a$ và $B N = C N = \frac{a}{2}$

$A O^{2} = A B^{2} - B O^{2} = A B^{2} - {(\frac{2}{3} B M)}^{2} = \frac{2}{3} a^{2} O N^{2} = B N^{2} + B O^{2} = \frac{7}{12} a^{2}; A N = \sqrt{A O^{2} + O N^{2}} = \frac{\sqrt{5}}{2} a \Rightarrow \cos α = \frac{A C^{2} + C N^{2} - A N^{2}}{2 A C . C N} = \frac{\sqrt{3}}{6}$

Câu 26:

Trong không gian cho hai tam giác đều ABC và ABC' có chung cạnh AB và nằm trong hai mặt phẳng khác nhau. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, CB, BC' và C'A. Hãy xác định góc giữa cặp vectơ

\vec{A B}

và

\vec{C C'}

?

A. 45°

B. 120°

C. 60°

D. 90°

Xem đáp án

Chọn C.

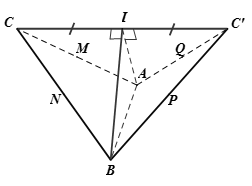
Trong không gian cho hai tam giác đều ABC và ABC' có chung cạnh AB và nằm trong hai mặt phẳng khác nhau. (ảnh 1)

Gọi I là trung điểm CC'

$Δ C A C^{'}$ cân tại A $\Rightarrow C C^{'} ⊥ A I (1)$

$Δ C B C^{'}$ cân tại B $\Rightarrow C C^{'} ⊥ B I (2)$

$\overset{(1), (2)}{\to} C C^{'} ⊥ (A I B) \Rightarrow C C^{'} ⊥ A B \Rightarrow \vec{C C^{'}} = \vec{A B}$

Kết luận: góc giữa và là

Câu 27:

Cho góc giữa

\vec{a} = 3,^{} \vec{b} = 5

và

\vec{a}

bằng

\vec{b}

. Chọn khẳng định sai trong các khẳng đính sau?

A. $|\vec{a} + \vec{b}| = \sqrt{19}$

B. $|\vec{a} - \vec{b}| = 7$

C. $|\vec{a} - 2 \vec{b}| = \sqrt{139}$

D. $|\vec{a} + 2 \vec{b}| = 9$

Xem đáp án

Chọn A.

Ta có:

{|\vec{a} + \vec{b}|}^{2} = {\vec{a}}^{2} + {\vec{b}}^{2} + 2 \vec{a} . \vec{b} . \cos (\vec{a}, \vec{b}) = 19

Câu 28:

Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ

\vec{A F}

và

\vec{E G}

?

A. 90°

B. 60°

C. 45°

D. 120°

Xem đáp án

Chọn B.

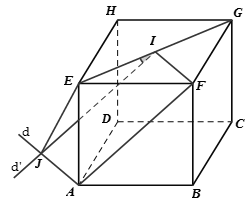
Cho hình lập phương ABCD.EFGH . Hãy xác định góc giữa cặp vectơ AF và vecto EG ? (ảnh 1)

Đặt cạnh của hình lập phương trên là a

Gọi I là giao trung điểm EG

Qua A kẻ đường thẳng d // FI

Qua I kẻ đường thẳng d' // FA

Suy ra d cắt d' tại J

Từ đó suy ra $(\hat{\vec{E G,} \vec{A F}}) = \hat{E I J} = α$

$I J = A F = 2 E I = 2 F I = 2 A J = a \sqrt{2} E J^{2} = A E^{2} + A J^{2} = \frac{3}{2} \cos α = |\frac{E I^{2} + I J^{2} + A J^{2}}{2. E I . E J}| = \frac{1}{2} \Rightarrow α = 60 °$

Câu 29:

Cho tứ diện ABCD có AB = AC = AD và $\hat{B A C} = \hat{B A D} = 60^{0}$ . Hãy xác định góc giữa cặp vectơ $\vec{A B}$ và $\vec{C D}$ ?

A. 60°

B. 45°

C. 120°

D. 90°

Xem đáp án

Chọn D

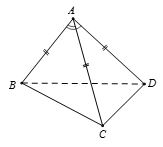
Cho tứ diện ABCD có AB = AC = AD và góc BAC = góc BAD = 60 độ. Hãy xác định góc giữa cặp vectơ AB và vecto CD ? (ảnh 1)

Ta có

$\begin{array}{l} \vec{A B} . \vec{C D} = \vec{A B} . (\vec{A D} - \vec{A C}) = \vec{A B} . \vec{A D} - \vec{A B} . \vec{A C} \\ = A B . A D . \cos 60^{0} - A B . A C . \cos 60^{0} = 0 \end{array} \Rightarrow (\vec{A B}, \vec{C D}) = 90^{0}$

Câu 30:

Cho hình lập phương $A B C D . A_{1} B_{1} C_{1} D_{1}$ . Góc giữa AC và DA₁ là

A. 45°

B. 60°

C. 60°

D. 120°

Xem đáp án

Chọn C

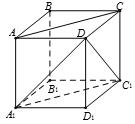
Cho hình lập phương ABCD.A1B1C1D1 . Góc giữa AC và DA1 là A. góc 45 độ B. góc 90 độ C. góc 60 độ D. góc 120 độ (ảnh 1)

Vì A'C' // AC nên góc giữa AC và DA₁ là $\hat{D A_{1} C_{1}}$

Vì tam giác $D A_{1} C_{1}$ đều nên $\hat{D A_{1} C_{1}} = 60^{0}$

Vậy góc giữa AC và DA₁ bằng 60°

Câu 31:

Cho hình chóp S.ABC có SA = SB = SC và $\hat{A S B} = \hat{B S C} = \hat{C S A}$ . Hãy xác định góc giữa cặp vectơ $\vec{S A}$ và $\vec{B C}$ ?

A. 120°

B. 90°

C. 60°

D. 45°

Xem đáp án

Chọn B

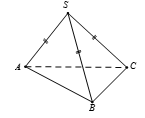
Cho hình chóp S.ABC có SA = SB = SC và góc ASB = góc BSC = góc CSA . Hãy xác định góc giữa cặp vectơ SA và vecto BC ? (ảnh 1)

Ta có

$\begin{array}{l} \vec{S A} . \vec{B C} = \vec{S A} . (\vec{S C} - \vec{S B}) = \vec{S A} . \vec{S C} - \vec{S A} . \vec{S B} \\ = S A . S C . \cos \hat{A S C} - S A . S B . \cos \hat{A S B} = 0 \end{array} \Rightarrow (\vec{S A}, \vec{B C}) = 90^{0}$

Câu 32:

Cho tứ diện đều ABCD , M là trung điểm của cạnh BC. Khi đó cos(AB, DM) bằng

A. $\frac{\sqrt{2}}{2}$

B. $\frac{\sqrt{3}}{6}$

C. $\frac{1}{2}$

D. $\frac{\sqrt{3}}{2}$

Xem đáp án

Chọn B

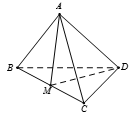
Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Khi đó cos(AB, DM) bằng (ảnh 1)

Giả sử cạnh của tứ diện là a

Ta có $\cos (\vec{A B}, \vec{D M}) = \frac{\vec{A B} . \vec{D M}}{|\vec{A B}| . |\vec{D M}|} = \frac{\vec{A B} . \vec{D M}}{a . \frac{a \sqrt{3}}{2}}$

Mặt khác

$\begin{array}{l} \vec{A B} . \vec{D M} = \vec{A B} (\vec{A M} - \vec{A D}) = \vec{A B} . \vec{A M} - \vec{A B} . \vec{A D} = A B . A M . \cos 30^{0} - A B . A D . \cos 60^{0} \\ = a . \frac{a \sqrt{3}}{2} . \frac{\sqrt{3}}{2} - a . a . \frac{1}{2} = \frac{3 a^{2}}{4} - \frac{a^{2}}{2} = \frac{a^{2}}{4} . \end{array}$

Do có $\cos (\vec{A B}, \vec{D M}) = \frac{\sqrt{3}}{6}$

Suy ra $\cos (A B, D M) = \frac{\sqrt{3}}{6}$

Câu 33:

Cho tứ diện ABCD có AB vuông góc với CD, AB = CD = 6. M là điểm thuộc cạnh BC sao cho MB = x.BC (0 < x < 1) . mp(P) song song với AB và CD lần lượt cắt BC, DB, AD, AC tại M, N, P, Q . Diện tích lớn nhất của tứ giác bằng bao nhiêu ?

A. 9

B. 11

C. 10

D. 8

Xem đáp án

Chọn A

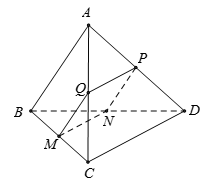
Cho tứ diện ABCD có AB vuông góc với CD, AB = CD = 6. M là điểm thuộc cạnh BC sao cho MB = x.BC (0 < x < 1) . mp(P) song song với AB và CD (ảnh 1)

Xét tứ giác MNPQ có $\{\begin{cases} M Q // N P // A B \\ M N // P Q // C D \end{cases}$

=> MNPQ là hình bình hành.

Mặt khác $A B ⊥ C D \Rightarrow M Q ⊥ M N$

Do đó, MNPQ là hình chữ nhật.

Vì $M Q // A B$ nên $\frac{M Q}{A B} = \frac{C M}{C B} = x \Rightarrow M Q = x . A B = 6 x$

Theo giả thiết $M C = x . B C \Rightarrow B M = (1 - x) B C$

Vì MN // CD nên $\frac{M N}{C D} = \frac{B M}{B C} = 1 - x \Rightarrow M N = (1 - x) . C D = 6 (1 - x)$

Diên tích hình chữ nhật MNPQ là

$S_{M N P Q} = M N . M Q = 6 (1 - x) .6 x = 36. x . (1 - x) \leq 36 {(\frac{x + 1 - x}{2})}^{2} = 9$

Ta có $S_{M N P Q} = 9$ khi $x = 1 - x \Leftrightarrow x = \frac{1}{2}$

Vậy diện tích tứ giác MNPQ lớn nhất bằng 9 khi M là trung điểm của BC

Câu 34:

Cho tứ diện ABCD đều cạnh bằng a . Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Góc giữa AO và CD bằng bao nhiêu ?

A. 0°

B. 30°

C. 90°

D. 60°

Xem đáp án

Chọn C

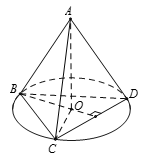
Cho tứ diện ABCD đều cạnh bằng a . Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Góc giữa AO và CD bằng bao nhiêu ? (ảnh 1)

Ta có $\vec{A O} . \vec{C D} = (\vec{C O} - \vec{C A}) \vec{C D}$

$\begin{array}{l} = \vec{C O} . \vec{C D} - \vec{C A} . \vec{C D} = C O . C D . \cos 30^{0} - C A . C D . \cos 60^{0} \\ = \frac{a \sqrt{3}}{3} . a . \frac{\sqrt{3}}{2} - a . a . \frac{1}{2} = \frac{a^{2}}{2} - \frac{a^{2}}{2} = 0. \end{array}$

Suy ra $A O ⊥ C D$

Câu 35:

Cho tứ diện ABCD có AB = CD . Gọi I, J, E, F lần lượt là trung điểm của AC, BC, BD, AD. Góc (IE, JF) bằng

A. 30°

B. 45°

C. 60°

D. 90°

Xem đáp án

Chọn D

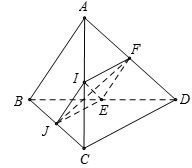
Cho tứ diện ABCD có AB = CD . Gọi I, J, E, F lần lượt là trung điểm của AC, BC, BD, AD. Góc (IE, JF) bằng (ảnh 1)

Tứ giác IJEF là hình bình hành.

Mặt khác $\{\begin{cases} I J = \frac{1}{2} A B \\ J E = \frac{1}{2} C D \end{cases}$ mà AB = CD nên IJ = JE.

Do đó IJEF là hình thoi.

Suy ra $(I E, J F) = 90^{0}$

Câu 36:

Cho tứ diện ABCD với

A C = \frac{3}{2} A D, \hat{C A B} = \hat{D A B} = 60^{0}, C D = A D

. Gọi

φ

là góc giữa AB và CD . Chọn khẳng định đúng ?

A. $\cos φ = \frac{3}{4}$

B. $φ = 60^{0}$

C. $φ = 30^{0}$

D. $\cos φ = \frac{1}{4}$

Xem đáp án

Chọn D

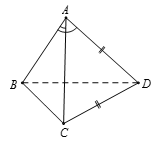
Cho tứ diện ABCD với AC = 3/2 AD, góc CAB = góc DAB = 60 độ, CD = AD. Gọi phi là góc giữa AB và CD . Chọn khẳng định đúng ? (ảnh 1)

Ta có $\cos (\vec{A B}, \vec{C D}) = \frac{\vec{A B} . \vec{C D}}{|\vec{A B}| . |\vec{C D}|} = \frac{\vec{A B} . \vec{C D}}{A B . C D}$

Mặt khác

$\begin{array}{l} \vec{A B} . \vec{C D} = \vec{A B} (\vec{A D} - \vec{A C}) = \vec{A B} . \vec{A D} - \vec{A B} . \vec{A C} \\ = A B . A D . \cos 60^{0} - A B . A C . \cos 60^{0} \\ = A B . A D . \frac{1}{2} - A B . \frac{3}{2} A D . \frac{1}{2} = - \frac{1}{4} A B . A D = - \frac{1}{4} A B . C D . \end{array}$

Do có $\cos (\vec{A B}, \vec{C D}) = \frac{- \frac{1}{4} A B . C D}{A B . C D} = - \frac{1}{4}$ . Suy ra $\cos φ = \frac{1}{4}$

Câu 37:

Trong không gian cho hai hình vuông ABCD và ABC'D' có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm O và O' . Tứ giác CDD'C' là hình gì?

A. Hình bình hành.

B. Hình vuông.

C. Hình thang.

D. Hình chữ nhật.

Xem đáp án

Chọn D

Tứ giác CDD'C' là hình bình hành. Lại có: $D C ⊥ (A D D') \Rightarrow D C ⊥ D D' .$

Vậy tứ giác CDD'C' là hình chữ nhật.

Câu 38:

Cho tứ diện ABCD có $A B = C D = a, IJ= \frac{a \sqrt{3}}{2}$ ( I, J lần lượt là trung điểm của BC và AD ). Số đo góc giữa hai đường thẳng AB và CD là :

A. 30°

B. 45°

C. 60°

D. 90°

Xem đáp án

Chọn C

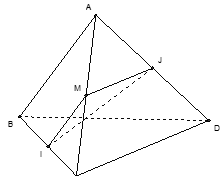
Gọi M là trung điểm của AC.

Góc giữa hai đường thẳng AB và CD bằng góc giữa hai đường thẳng MI và MJ.

Tính được: $\cos IMJ = \frac{I M^{2} + M J^{2} - {IJ}^{2}}{2 M I . M J} = - \frac{1}{2}$

Từ đó suy ra số đo góc giữa hai đường thẳng AB và CD là: $60^{0} .$

Câu 39:

Cho tứ diện ABCD với

A B ⊥ A C, A B ⊥ B D

. Gọi P, Q lần lượt là trung điểm của AB và CD. Góc giữa PQ và AB là?

A. 90°

B. 60°

C. 30°

D. 45°

Xem đáp án

Chọn A

$\vec{A B} . \vec{P Q} \Rightarrow A B ⊥ P Q$

Câu 40:

Cho hai vectơ

\vec{a}, \vec{b}

thỏa mãn:

|\vec{a}| = 4; |\vec{b}| = 3; |\vec{a} - \vec{b}| = 4

. Gọi

α

là góc giữa hai vectơ

\vec{a}, \vec{b}

. Chọn khẳng định đúng?

A. $\cos α = \frac{3}{8}$

B. $α = 30^{0}$

C. $\cos α = \frac{1}{3}$

D. $α = 60^{0}$

Xem đáp án

Chọn A

${(\vec{a} - \vec{b})}^{2} = {|\vec{a}|}^{2} + {|\vec{b}|}^{2} - 2 \vec{a} . \vec{b} \Rightarrow \vec{a} . \vec{b} = \frac{9}{2} .$

Do đó: $\cos α = \frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|} = \frac{3}{8}$

Câu 41:

Cho tứ diện ABCD. Tìm giá trị của k thích hợp thỏa mãn: $\vec{A B} . \vec{C D} + \vec{A C} . \vec{D B} + \vec{A D} . \vec{B C} = k$

A. k = 1

B. k = 2

C. k = 0

D. k = 4

Xem đáp án

Chọn C

$\begin{array}{l} \vec{A B} . \vec{C D} + \vec{A C} . \vec{D B} + \vec{A D} . \vec{B C} = (\vec{A C} + \vec{C B}) . \vec{C D} + \vec{A C} . \vec{D B} - \vec{A D} . \vec{C B} \\ = \vec{A C} (\vec{C D} + \vec{D B}) + \vec{C B} (\vec{C D} - \vec{A D}) = \vec{A C} . \vec{C B} + \vec{C B} . \vec{A C} = 0. \end{array}$

Câu 42:

Trong không gian cho tam giác ABC có trọng tâm G. Chọn hệ thức đúng?

A. $A B^{2} + A C^{2} + B C^{2} = 2 (G A^{2} + G B^{2} + G C^{2}) .$

B. $A B^{2} + A C^{2} + B C^{2} = G A^{2} + G B^{2} + G C^{2} .$

C. $A B^{2} + A C^{2} + B C^{2} = 4 (G A^{2} + G B^{2} + G C^{2}) .$

D. $A B^{2} + A C^{2} + B C^{2} = 3 (G A^{2} + G B^{2} + G C^{2}) .$

Xem đáp án

Chọn D

Cách 1

Ta có

$\begin{array}{l} {(\vec{G A} + \vec{G B} + \vec{G C})}^{2} = 0 \\ \Leftrightarrow G A^{2} + G B^{2} + G C^{2} + 2 \vec{G A} . \vec{G B} + 2 \vec{G A} . \vec{G C} + 2 \vec{G B} . \vec{G C} = 0 \\ \Leftrightarrow G A^{2} + G B^{2} + G C^{2} + (G A^{2} + G B^{2} - A B^{2}) + (G A^{2} + G C^{2} - A C^{2}) + (G B^{2} + G C^{2} - B C^{2}) = 0 \\ \Leftrightarrow A B^{2} + A C^{2} + B C^{2} = 3 (G A^{2} + G B^{2} + G C^{2}) \end{array}$

Cách 2: Ta có:

$\{\begin{cases} M A^{2} = \frac{A B^{2} + A C^{2}}{2} - \frac{B C^{2}}{4} \\ G A = \frac{2}{3} M A \end{cases} \Rightarrow G A^{2} = \frac{4}{9} (\frac{A B^{2} + A C^{2}}{2} - \frac{B C^{2}}{4}) .$

Tương tự ta suy ra được

\begin{array}{l} G A^{2} + G B^{2} + G C^{2} = \frac{4}{9} (\frac{A B^{2} + A C^{2}}{2} - \frac{B C^{2}}{4} + \frac{B A^{2} + B C^{2}}{2} - \frac{A C^{2}}{4} + \frac{C A^{2} + C B^{2}}{2} - \frac{A B^{2}}{4}) . \\ = \frac{1}{3} (A B^{2} + B C^{2} + C A^{2}) . \\ \Leftrightarrow 3 (G A^{2} + G B^{2} + G C^{2}) = A B^{2} + B C^{2} + C A^{2} \end{array}

Cách 3: Chuẩn hóa giả sử tam giác ABC đều có cạnh là 1. Khi đó

$\{\begin{cases} A B^{2} + B C^{2} + C A^{2} = 3 \\ G A^{2} + G B^{2} + G C^{2} = 1 \end{cases} \Rightarrow 3 (G A^{2} + G B^{2} + G C^{2}) = A B^{2} + B C^{2} + C A^{2} .$

Câu 43:

Trong không gian cho tam giác ABC. Tìm M sao cho giá trị của biểu thức

P = M A^{2} + M B^{2} + M C^{2}

đạt giá trị nhỏ nhất.

A. M là trọng tâm tam giác ABC.

C. M là trực tâm tam giác ABC.

D. M là tâm đường tròn nội tiếp tam giác ABC.

Xem đáp án

Chọn A

Gọi G là trọng tâm tam giác ABC => G cố định và $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0} .$

$\begin{array}{l} P = {(\vec{M G} + \vec{G A})}^{2} + {(\vec{M G} + \vec{G B})}^{2} + {(\vec{M G} + \vec{G C})}^{2} \\ = 3 M G^{2} + 2 \vec{M G} . (\vec{G A} + \vec{G B} + \vec{G C}) + G A^{2} + G B^{2} + G C^{2} \\ = 3 M G^{2} + G A^{2} + G B^{2} + G C^{2} \geq G A^{2} + G B^{2} + G C^{2} . \end{array}$

Dấu bằng xảy ra $\Leftrightarrow M \equiv G .$

Vậy $P_{\min} = G A^{2} + G B^{2} + G C^{2}$ với $M \equiv G$ là trọng tâm tam giác ABC

Câu 44:

Cho hai vectơ $\vec{a}, \vec{b}$ thỏa mãn: $|\vec{a}| = 26; |\vec{b}| = 28; |\vec{a} + \vec{b}| = 48$ . Độ dài vectơ $\vec{a} - \vec{b}$ bằng?

A. 25

B. $\sqrt{616}$

C. 9

D. $\sqrt{618}$

Xem đáp án

Chọn B

$\begin{array}{l} {|\vec{a} - \vec{b}|}^{2} = {(\vec{a} - \vec{b})}^{2} = {\vec{a}}^{2} + {\vec{b}}^{2} - 2 \vec{a} . \vec{b} = 2 ({\vec{a}}^{2} + {\vec{b}}^{2}) - {(\vec{a} + \vec{b})}^{2} \\ = 2 ({|\vec{a}|}^{2} + {|\vec{b}|}^{2}) - {|\vec{a} + \vec{b}|}^{2} = 2 (26^{2} + 28^{2}) - 48^{2} = 616 \\ \Rightarrow |\vec{a} - \vec{b}| = \sqrt{616} . \end{array}$

Câu 45:

Cho tứ diện ABCD có DA = DB = DC và

\hat{B D A} = 60^{0}, \hat{A D C} = 90^{0}, \hat{B D C} = 120^{0}

. Trong các mặt của tứ diện đó:

A. Tam giác ABD có diện tích lớn nhất.

B. Tam giác BCD có diện tích lớn nhất.

C. Tam giác ACD có diện tích lớn nhất.

D. Tam giác ABC có diện tích lớn nhất.

Xem đáp án

Chọn D

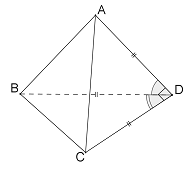
Cho tứ diện ABCD có DA = DB = DC và góc BDA = 60 độ, góc ADC = 90 độ, góc BDC = 120 độ. Trong các mặt của tứ diện đó: (ảnh 1)

Đặt $D A = D B = D C = a$

Tam giác ABD đều cạnh a nên diện tích $S_{A B D} = \frac{a^{2} \sqrt{3}}{4}$ .

Tam giác ACD vuông tại D nên diện tích $S_{A C D} = \frac{1}{2} D A . D C = \frac{a^{2}}{2}$ .

Diện tích tam giác BCD là $S_{B C D} = \frac{1}{2} D B . D C \sin 120^{0} = \frac{a^{2} \sqrt{3}}{4}$ .

Tam giác ABC có $A B = a, A C = a \sqrt{2}, B C = a \sqrt{3}$ nên tam giác ABC vuông tại A .

Diện tích tam giác ABC là $S_{A B C} = \frac{1}{2} A B . A C = \frac{a^{2} \sqrt{2}}{2}$ .

Vậy diện tích tam giác ABC lớn nhất.

Câu 46:

Cho hai vectơ $\vec{a}, \vec{b}$ thỏa mãn: $|\vec{a}| = 4; |\vec{b}| = 3; \vec{a} . \vec{b} = 10$ . Xét hai vectơ $\vec{y} = \vec{a} - \vec{b}, \vec{x} = \vec{a} - 2 \vec{b}$ . Gọi α là góc giữa hai vectơ $\vec{x}, \vec{y}$ . Chọn khẳng định đúng.

A. $\cos α = \frac{- 2}{\sqrt{15}}$

B. $\cos α = \frac{1}{\sqrt{15}}$

C. $\cos α = \frac{3}{\sqrt{15}}$

D. $\cos α = \frac{2}{\sqrt{15}}$

Xem đáp án

Chọn D

Ta có: $\vec{x} . \vec{y} = (\vec{a} - 2 \vec{b}) (\vec{a} - \vec{b}) = {(\vec{a})}^{2} + 2 {(\vec{b})}^{2} - 3 \vec{a} . \vec{b} = 4$

$|\vec{x}| = \sqrt{{(\vec{x})}^{2}} = \sqrt{{(\vec{a} - 2 \vec{b})}^{2}} = \sqrt{{(\vec{a})}^{2} + 4 {(\vec{b})}^{2} - 4 \vec{a} . \vec{b}} = 2 \sqrt{3} |\vec{y}| = \sqrt{{(\vec{y})}^{2}} = \sqrt{{(\vec{a} - \vec{b})}^{2}} = \sqrt{{(\vec{a})}^{2} + {(\vec{b})}^{2} - 2 \vec{a} . \vec{b}} = \sqrt{5} \cos α = \frac{\vec{x} . \vec{y}}{|\vec{x}| . |\vec{y}|} = \frac{4}{2 \sqrt{3} . \sqrt{5}} = \frac{2}{\sqrt{15}}$

Câu 47:

Cho tam giác ABC có diện tích S. Tìm giá trị của k thích hợp thỏa mãn:

S = \frac{1}{2} \sqrt{{\vec{A B}}^{2} . {\vec{A C}}^{2} - 2 k {(\vec{A B} . \vec{A C})}^{2}}

A. $k = \frac{1}{4}$

B. k = 0

C. $k = \frac{1}{2}$

D. k = 1

Xem đáp án

Chọn C

$S = \frac{1}{2} A B . A C . \sin C = \frac{1}{2} \sqrt{A B^{2} . A C^{2} \sin^{2} C} = \frac{1}{2} \sqrt{A B^{2} . A C^{2} (1 - \cos^{2} C)} = \frac{1}{2} \sqrt{{\vec{A B}}^{2} . {\vec{A C}}^{2} - {(\vec{A B} . \vec{A C})}^{2}}$

Câu 48:

Cho hình chóp S.ABC có SA = SB = SC = a và

B C = a \sqrt{2}

. Tính góc giữa hai đường thẳng AB và SC

A. $\hat{(A B, S C)} = 60^{0}$

B. $\hat{(A B, S C)} = 45^{0}$

C. $\hat{(A B, S C)} = 30^{0}$

D. $\hat{(A B, S C)} = 90^{0}$

Xem đáp án

Chọn A

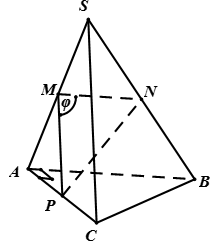
Cho hình chóp S.ABC có SA = SB = SC = a và BC = a căn bậc hai 2 Tính góc giữa hai đường thẳng AB và SC (ảnh 1)

Gọi M, N, P lần lượt là trung điểm của SA, SB, AC, khi đó MN // AB nên $\hat{(A B, S C)} = \hat{(M N, S C)}$

Đặt $φ = \hat{N M P}$ , trong tam giác MNP có $\cos φ = \frac{M N^{2} + M P^{2} - N P^{2}}{2 M N . M P} (1)$

Ta có $M N = M P = \frac{a}{2}, A B^{2} + A C^{2} = B C^{2} \Rightarrow Δ A B C$ vuông tại A, vì vậy $P B^{2} = A P^{2} + A C^{2} = \frac{5 a^{2}}{4}, P S^{2} = \frac{3 a^{2}}{4}$

Trong tam giác PBS theo công thứ tính đường trung tuyến ta có $P N^{2} = \frac{P B^{2} + P S^{2}}{2} - \frac{S B^{2}}{4} = \frac{\frac{5 a^{2}}{4} + \frac{3 a^{2}}{4}}{2} - \frac{a^{2}}{4} = \frac{3 a^{2}}{4}$

Thay MN, MP, NP vào (1) ta được $\cos φ = - \frac{1}{2} \Rightarrow φ = 120^{0}$

Vậy $\hat{(A B, S C)} = \hat{(M N, S C)} = 60^{0}$

Câu 49:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi, SA = AB và $S A ⊥ B C$ . Tính góc giữa hai đường thẳng SD và BC .

A. $\hat{(B C, S D)} = 30^{0}$

B. $\hat{(B C, S D)} = 45^{0}$

C. $\hat{(B C, S D)} = 60^{0}$

D. $\hat{(B C, S D)} = 50^{0}$

Xem đáp án

Chọn B

Câu 50:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi, SA = AB và $S A ⊥ B C$ . Gọi I, J lần lượt là các điểm thuộc SB và SD sao cho IJ // BD. Chứng minh góc giữa AC và IJ không phụ thuộc vào vị trí của I và J.

A. $\hat{(I J, A C)} = 90^{0}$

B. $\hat{(I J, A C)} = 60^{0}$

C. $\hat{(I J, A C)} = 30^{0}$

D. $\hat{(I J, A C)} = 45^{0}$

Xem đáp án

Chọn A

Câu 51:

Cho hai tam giác cân ABC và DBC có chung cạnh đáy BC nằm trong hai mặt phẳng khác nhau.

a) Khẳng định nào sau đây là đúng nhất?

A. $A D ⊥ B C$

B. AD cắt BC

C. AD và BC chéo nhau

D. Cả A, B, C đều đúng

Xem đáp án

Chọn A

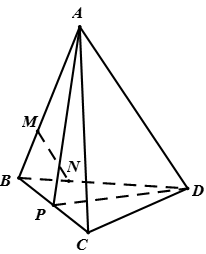
Cho hai tam giác cân ABC và DBC có chung cạnh đáy BC nằm trong hai mặt phẳng khác nhau. a) Khẳng định nào sau đây là đúng nhất? (ảnh 1)

a) Gọi P là trung điểm của BC, thì các tam giác ABC và DBC cân nên $\{\begin{cases} A P ⊥ B C \\ D P ⊥ B C \end{cases}$

Ta có $\vec{B C} . \vec{A D} = \vec{B C} (\vec{P D} - \vec{P A}) = 0$

Vậy $B C ⊥ A D$

Câu 52:

b) Gọi M, N là các điểm lần lượt thuộc các đường thẳng AB và DB sao cho

\vec{M A} = k \vec{M B}, \vec{N D} = k \vec{N B}

. Tính góc giữa hai đường thẳng MN và BC .

A. $\hat{(M N, B C)} = 90^{0}$

B. $\hat{(M N, B C)} = 80^{0}$

C. $\hat{(M N, B C)} = 60^{0}$

D. $\hat{(M N, B C)} = 45^{0}$

Xem đáp án

Chọn A

b) Ta có $\vec{M A} = k \vec{M B} \Rightarrow \frac{M A}{M B} = |k|, \vec{N D} = k \vec{N B} \Rightarrow \frac{N D}{N B} = |k|$

$\Rightarrow \frac{M A}{M B} = \frac{N D}{N B}$

suy ra $M N ∥ A D \Rightarrow \hat{(M N, B C)} = \hat{(A D, B C)} = 90^{0}$ ( Theo câu a)

Câu 53:

Cho tứ diện ABCD . Gọi M, N lần lượt là trung điểm các cạnh BC và AD . Cho biết AB = CD = 2a và

M N = a \sqrt{3}

. Tính góc giữa hai đường thẳng AB và CD .

A. $\hat{(A B, C D)} = 30^{0}$

B. $\hat{(A B, C D)} = 45^{0}$

C. $\hat{(A B, C D)} = 60^{0}$

D. $\hat{(A B, C D)} = 90^{0}$

Xem đáp án

Chọn C

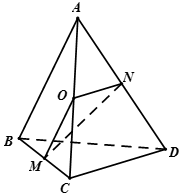
Cho tứ diện ABCD . Gọi M, N lần lượt là trung điểm các cạnh BC và AD. Cho biết AB = CD = 2a và MN = a căn bậc hai 3 (ảnh 1)

Gọi O là trung điểm của AC, ta có OM = ON = a.

$\{\begin{cases} O M ∥ A B \\ O N ∥ C D \end{cases} \Rightarrow \hat{(A B, C D)} = \hat{(O M, O N)}$

Áp dụng định lí côsin cho tam giác OMN ta có

$\cos \hat{M O N} = \frac{O M^{2} + O N^{2} - M N^{2}}{2 O M . O N} = \frac{a^{2} + a^{2} - {(a \sqrt{3})}^{2}}{2. a . a} = - \frac{1}{2}$

Vậy $\hat{(A B, C D)} = 60^{0}$

Câu 54:

Cho tứ diện ABCD có AB = CD = a, AC = BD = b, AD = BC = c.

a) Khẳng định nào sau đây là đúng nhất.

A. các đoạn nối trung điểm các cặp cạnh đối thì vuông góc với hai cạnh đó

B. các đoạn nối trung điểm các cặp cạnh đối thì không vuông góc với hai cạnh đó

C. các đoạn nối trung điểm các cặp cạnh đối thì có thể vuông góc có thể không vuông góc với hai cạnh đó

D. cả A, B, C đều sai

Xem đáp án

Chọn A

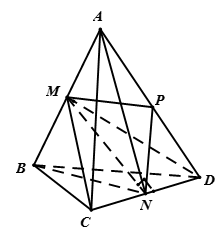
Cho tứ diện ABCD có AB = CD = a, AC = BD = b, AD = BC = c. a)Khẳng định nào sau đây là đúng nhất. (ảnh 1)

Gọi M, N, P lần lượt là trung điểm của các cạnh AB, CD, AD .

a) Do hai tam giác ACD và BCD có CD chung và AC = BD, AD = BC nên chúng bằng nhau, suy ra MC = MD

Vậy tam giác MCD cân tại M và có trung tuyến MN nên $M N ⊥ C D$

Tương tự $M N ⊥ A B$

Chứng minh tương tự cho hai cặp cạnh đối còn lại.

Câu 55:

b) Tính góc giữa hai đường thẳng AC và BD.

A. $\hat{(A C, B D)} = \arccos |\frac{(a^{2} - c^{2})}{b^{2}}|$

B. $\hat{(A C, B D)} = \arccos |\frac{2 (a^{2} + c^{2})}{b^{2}}|$

C. $\hat{(A C, B D)} = \arccos |\frac{2 (a^{2} - c^{2})}{3 b^{2}}|$

D. $\hat{(A C, B D)} = \arccos |\frac{2 (a^{2} - c^{2})}{b^{2}}|$

Xem đáp án

Chọn D

b) Ta có $\{\begin{cases} P M ∥ B D \\ P N ∥ A C \end{cases} \Rightarrow \hat{(B D, A C)} = \hat{(P M, P N)}$

Theo công thức tính đường trung tuyến ta có $C M^{2} = \frac{C A^{2} + C B^{2}}{2} - \frac{A B^{2}}{4} = \frac{2 (b^{2} + c^{2}) - a^{2}}{4}$

Tương tự $D M^{2} = \frac{2 (b^{2} + c^{2}) - a^{2}}{4}$ , nên $M N^{2} = \frac{M C^{2} + M D^{2}}{2} - \frac{C D^{2}}{4} = \frac{2 (b^{2} + c^{2}) - a^{2}}{4} - \frac{a^{2}}{4} = \frac{b^{2} + c^{2} - a^{2}}{2}$

Áp dụng định lí cô sin cho tam giác PMN ta có $\cos \hat{M P N} = \frac{P M^{2} + P N^{2} - M N^{2}}{2. P M . P N} = \frac{{(\frac{b}{2})}^{2} + {(\frac{b}{2})}^{2} - \frac{b^{2} + c^{2} - a^{2}}{2}}{2 (\frac{b}{2}) (\frac{b}{2})} = \frac{2 (a^{2} - c^{2})}{b^{2}}$

Vậy $\hat{(A C, B D)} = \arccos |\frac{2 (a^{2} - c^{2})}{b^{2}}|$