A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C.
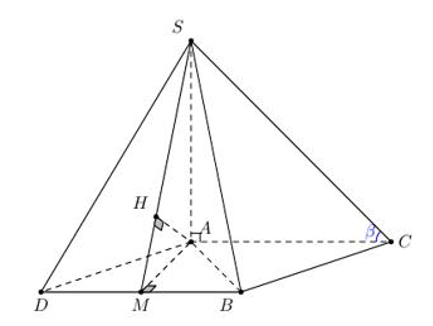
Do nên góc giữa SC và mặt phẳng (ABC) là góc Suy ra .
Trong tam giác SCA vuông tại A có
Lấy điểm D sao cho ABCD là hình bình hành.
Khi đó .
Ta có đều cạnh a.
Gọi M là trung điểm BD Suy ra và .
Trong kẻ với
Do .
Suy ra
Trong vuông tại A ta có:
.
Vậy
Cho khối chóp S.ABC có đáy là tam giác ABC cân tại A, , AB = a. Cạnh bên SA vuông góc với mặt đáy, SA = a Thể tích khối chóp đã cho bằng
Cho hàm bậc ba y=f(x) có đồ thị đạo hàm y=f '(x) như hình sau.
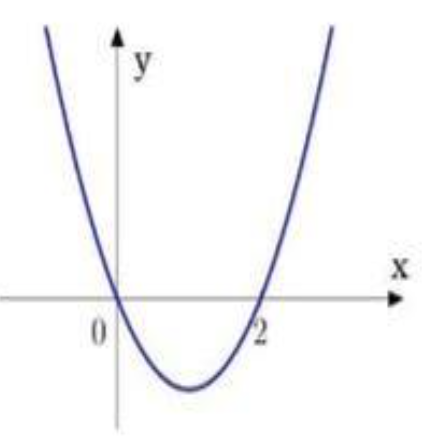
Hàm số đã cho nghịch biến trên khoảng
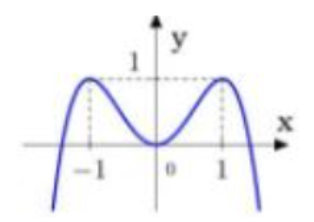
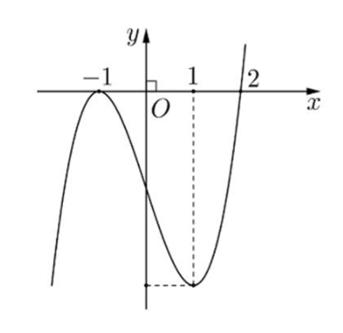
Cho hàm bậc bốn trùng phương y=f(x) có đồ thị như hình vẽ. Số nghiệm của phương trình là
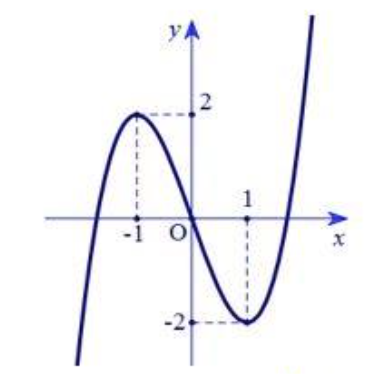
Tất cả các giá trị của tham số m để hàm số có hai điểm cực trị là
Cho hàm số f(x) liên tục trên R và có đồ thị hàm số f'(x) như hình vẽ. Gọi S là tập hợp các giá trị nguyên của tham số để hàm số nghịch biến trên khoảng Tổng giá trị các phần tử của S bằng
Trong không gian với trục tọa độ Oxyz cho mặt phẳng (P): 2x-3y+2z+4=0. Vectơ nào sau đây là một vectơ pháp tuyến của mặt phẳng (P)?
Trong không gian với hệ tọa độ Oxyz cho hai vectơ với m là tham số nhận giá trị thực. Tìm giá trị của m để hai vectơ và vuông góc với nhau
Cho hình nón có chiều cao h, đường sinh l và bán kính đường tròn đáy bằng R. Diện tích toàn phần của hình nón bằng
Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, Góc giữa hai mặt phẳng và là . Tính bán kính mặt cầu ngoại tiếp hình chóp S. ABCD.