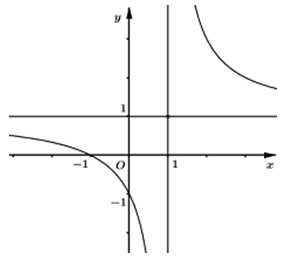
Cho hình trụ có diện tích toàn phần là $4\mathrm{\pi }$ và có thiết diện cắt bởi mặt phẳng qua trục là hình vuông. Tính thể tích khối trụ.

Hàm số nào sau đây có đồ thị phù hợp với hình vẽ?

Tìm hệ số của số hạng chứa $x^3$ trong khai triển Newton của ${\left(x+\frac{2}{\sqrt{x}}\right)}^6,x>0$.

Cho hình nón (N) đỉnh S có bán kính đáy bằng a và diện tích xung quanh $S_{xq}=2\pi a^2$. Tính thể tích V của khối chóp tứ giác đều S. ABCD có đáy ABCD nội tiếp đáy của khối nón (N).

Cho hình chóp S. ABCD có đáy là hình bình hành. Gọi G là trọng tâm tam giác SAB và M,N lần lượt là trung điểm của SC, SD. Biết thể tích khối chop S. ABCD là V, tính thể tích khối chóp S. GMN

Cho hình lăng trụ ABC.A'B'C có đáy là tam giác đều cạnh a. Mặt bên BB'C'C' là hình thoi và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa CC' và mặt phẳng (ABB'A) bằng $\frac{a\sqrt{12}}{5}$. Thể tích khối lăng trụ ABC.A'B'C bằng:

Cho hình lập phương $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ cạnh a. Gọi M là trung điểm cạnh C'D', G là trọng tâm tam giác ABD. Tính khoảng cách từ C đến mặt phẳng $\left(B^{\text{'}}MG\right)$.

Cho biểu thức $P=\sqrt[4]{x^2\sqrt[3]{x}} , \left(x>0\right)$. Mệnh đề nào dưới đây đúng?

Tính tổng T tất cả các nghiệm của phương trình ${4.9}^x-{13.6}^x+{9.4}^x=0.$ 

Cho bất phương trình ${\log }_3\left(x^2+2x+2\right)+1>{\log }_3\left(x^2+6x+5+m\right)$. Có tất cả bao nhiêu giá trị nguyên của tham số m để bất phương trình trên nghiệm đúng với mọi $x\in \left(1;3\right)$?

Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng 2a, cạnh bên bằng $a\sqrt{3}$ . Tính thể tích Vcủa khối cầu ngoại tiếp hình chóp S. ABCD.