Tổng tất cả các giá trị của tham số m để phương trình có đúng ba nghiệm phân biệt là
A. 2
B. 3
C. 1
D. 0
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn B
Phương trình tương đương .
.
Xét hàm đặc trưng là hàm số đồng biến nên từ phương trình suy ra .
Có .
và .
Xét các trường hợp sau:
Trường hợp 1: ta có bảng biến thiên của như sau:
Phương trình chỉ có tối đa 2 nghiệm nên không có m thoả mãn.
Trường hợp 2: tương tự.
Trường hợp 3: , bảng biến thiên như sau:
Phương trình có 3 nghiệm khi .
Cả 3 giá trị trên đều thoả mãn, nên tổng của chúng bằng 3.
Cho hàm số , hàm số có đồ thị như hình bên. Hàm số có bao nhiêu điểm cực trị trên khoảng .
Cho hàm số có bảng biến thiên như sau:
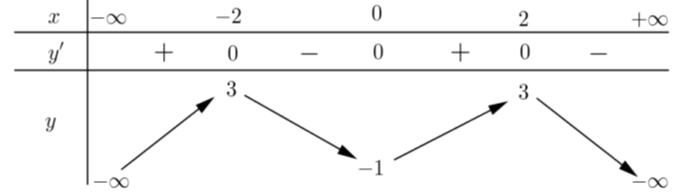
Cho hàm số có bảng biến thiên dưới đây
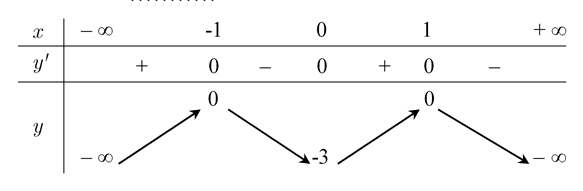
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
Trong không gian , cho hai điểm và . Phương trình mặt cầu có tâm I và đi qua A là
Trong không gian , cho ba điểm , , và mặt phẳng . Xét điểm M thay đổi thuộc , tìm giá trị nhỏ nhất của biểu thức .