Khoảng cách từ điểm M(5; – 1) đến đường thẳng d: 3x + 2y + 13 = 0 là
A. \(2\sqrt {13} \);
B. \(\frac{{28}}{{\sqrt {13} }}\);
C. 26;
D. \(\frac{{\sqrt {13} }}{2}\).
Giải bởi Vietjack
Tọa độ giao điểm của hai đường thẳng x – 3y – 6 = 0 và 3x + 4y – 1 = 0 là
Cho n là số tự nhiên. Hãy tính tổng sau:
S = \(C_{2n + 1}^0 + C_{2n + 1}^1 + C_{2n + 1}^2 + ... + C_{2n + 1}^n\).
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 2), B(3; 1) và C(5; 4). Phương trình nào sau đây là phương trình đường cao kẻ từ A của tam giác ABC?
Phương trình tổng quát của đường thẳng d đi qua điểm A(1; – 3) và nhận \(\overrightarrow n = \left( { - 2;\,\,7} \right)\) làm vectơ pháp tuyến là
Với n là số nguyên dương tùy ý lớn hơn 1, mệnh đề nào dưới đây đúng?
Một nhóm học sinh gồm 15 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành một đội cờ đỏ sao cho phải có 1 đội trưởng nam, 1 đội phó nam và có ít nhất 1 nữ. Hỏi có bao nhiêu cách lập đội cờ đỏ?
Phương tiện bạn Khoa có thể chọn đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt được thể hiện qua sơ đồ cây sau:
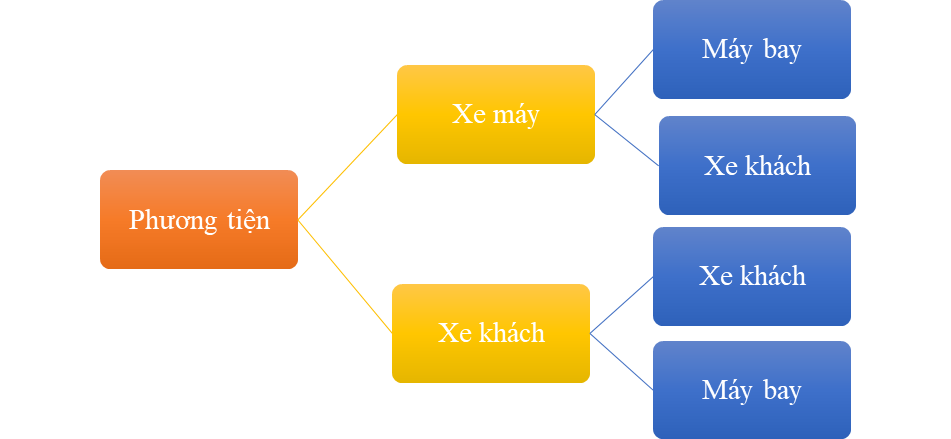
Hỏi bạn Khoa có mấy cách chọn phương tiện đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt?
Một lớp có 40 học sinh gồm 25 nam và 15 nữ. Hỏi có bao nhiêu cách chọn ra một nhóm 3 học sinh trong đó có ít nhất một học sinh nữ?
Cho hai vectơ \(\overrightarrow x = \left( {3;\, - 4} \right)\), \(\overrightarrow y = \left( { - 6;\,\,8} \right)\). Khẳng định nào sau đây là đúng?
Cho đường thẳng ∆ đi qua điểm A(4; – 5) và có một vectơ pháp tuyến là \(\overrightarrow n = \left( {1;\,\,2} \right)\). Phương trình tham số của đường thẳng ∆ là
Trong mặt phẳng tọa độ Oxy, cho hai vectơ \(\overrightarrow a = \left( {4;\,\, - m} \right)\) và \(\overrightarrow b = \left( {2m + 6;\,\,1} \right)\). Tập giá trị của m để hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương là
Trong mặt phẳng tọa độ Oxy, cho điểm H(1; 6). Tọa độ của vectơ \(\overrightarrow {OH} \) là
Có bao nhiêu cách xếp 5 người ngồi vào một dãy ghế gồm có 6 chiếc ghế, biết mỗi người ngồi vào một ghế.
Cho tập hợp H = {1; 3; 5; 7; 9; 11}. Một tổ hợp chập 3 của 6 phần tử của H là
