Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E lần lượt là trung điểm các cạnh AB và AC
a) Chứng minh tam giác ADE bằng tam giác HDE. Suy ra tứ giác ADHE nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác đó.
Giải bởi Vietjack
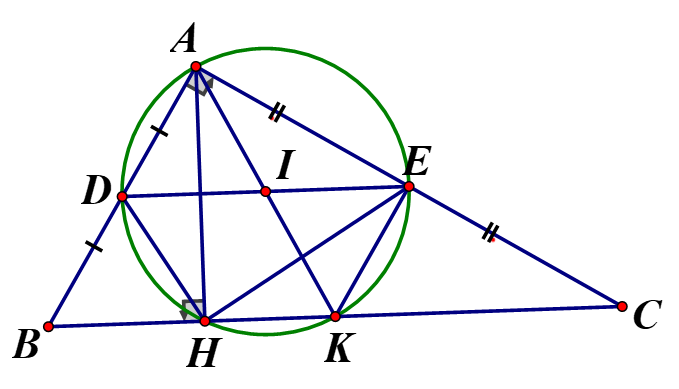
a) Xét và có:
DA = DH (tính chất đường trung tuyến ứng với cạnh huyền)
HE = AE (tính chất đường trung tuyến ứng với cạnh huyền)
DE chung
là tứ giác nội tiếp có tâm I là trung điểm DE
Giải bài toán bằng cách lập phương trình:
Một tam giác vuông có độ dài cạnh huyền bằng 10 cm và chu vi bằng 24 cm. Tính độ dài các cạnh góc vuông.
b) Đường tròn (I) cắt BC tại một điểm thứ hai là K ( ). Chứng minh K là trung điểm BC.
