Cho đường tròn (O) đường kính BC = 2R và A là một điểm nằm ngoài đường tròn. Các tia BA, CA cắt (O) theo thứ tự tại E và F, EC cắt BF tại H, tia AH cắt BC tại K.
a) Chứng minh và tứ giác HEBK nội tiếp Giải bởi Vietjack
Giải bởi Vietjack
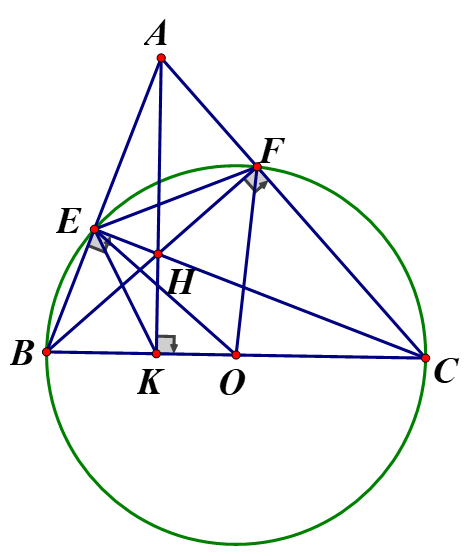
a) Ta có (góc nội tiếp chắn nửa đường tròn)
là trực tâm
Và suy ra BEHK là tứ giác nội tiếpb) Xác định hàm số y = ax2 biết đồ thị hàm số đi qua điểm M (-2;2). Vẽ đồ thị hàm số ứng với a tìm được.