Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn tâm O; các đường cao AM, CP và BN cắt nhau tại H.
a) Chứng minh các tứ giác APHN và HNCM nội tiếp
 Giải bởi Vietjack
Giải bởi Vietjack
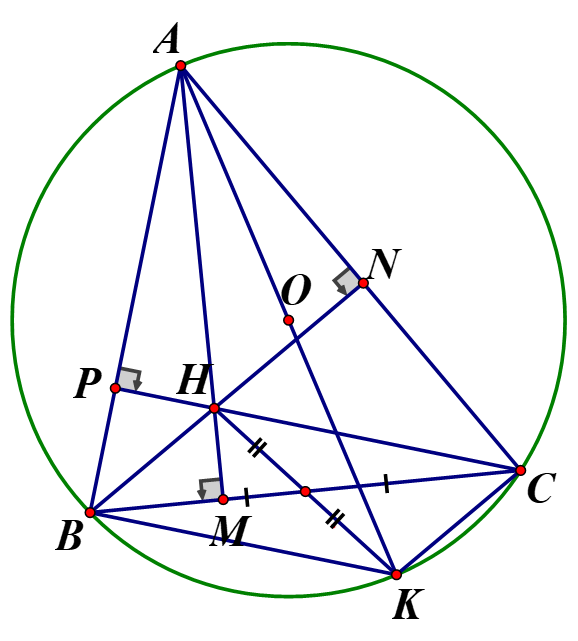
a) Ta có là tứ giác nội tiếp
là tứ giác nội tiếp