Cho hàm số bậc ba có đồ thị như hình vẽ.
![Cho hàm số bậc ba f(x)= ax^3+bx^2+cx+d có đồ thị như hình vẽ. Đồ thị hàm số g(x)= ( x^2-3x+2) căn x-1/ x [f^2(x)-f(x)] có bao nhiêu (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid5-1674808525.png)
Đồ thị hàm số có bao nhiêu đường tiệm cận đứng?
A. 4
B. 6
C. 3
D. 5
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Điều kiện xác định .
Xét phương trình .
Dựa vào đồ thị ta thấy
- Phương trình (1) có hai nghiệm phân biệt (loại) và (nghiệm kép).
- Phương trình (2) có ba nghiệm phân biệt , , .
Khi đó
Suy ra ,
trong đó , , nên đồ thị hàm số có ba tiệm cận đứng là x=2 ; ; .
Chọn C.
Biết đồ thị hàm số nhận trục hoành và trục tung làm hai tiệm cận thì giá trị bằng
Tất cả các giá trị thực của tham số m để đồ thị hàm số có đúng hai đường tiệm cận là
Cho hàm số xác định trên , có đạo hàm trên và có bảng biến thiên như sau
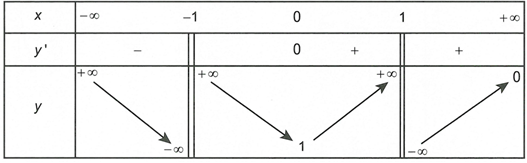
Đồ thị hàm số có bao nhiêu tiệm cận đứng và tiệm cận ngang?
Khoảng cách từ gốc tọa độ đến giao điểm của hai đường tiệm cận của đồ thị hàm số bằng
Cho hàm số . Gọi I là giao điểm của hai tiệm cận của đồ thị hàm số . Khoảng cách từ I đến tiếp tuyến bất kỳ của đồ thị đạt giá trị lớn nhất bằng
Cho hàm số (C). Gọi M là điểm bất kỳ trên , d là tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị. Giá trị nhỏ nhất của d bằng
Các đường tiệm cận của đồ thị hàm số tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng
Cho hàm số có đồ thị . Hai đường tiệm cận của (C) cắt nhau tại I. Đường thẳng (b là tham số thực) cắt đồ thị(C) tại hai điểm phân biệt A, B. Biết và diện tích tam giác AIB bằng . Giá trị của b bằng
Cho hàm số y= f(x) có bảng biến thiên như sau
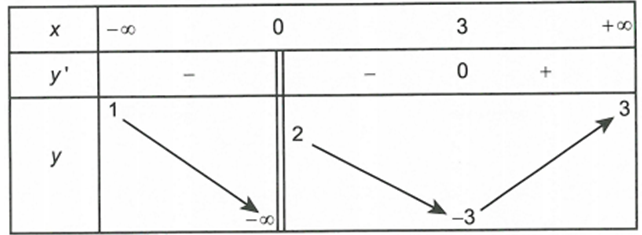
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
Biết đồ thị hàm số nhận trục hoành và trục tung làm hai tiệm cận. Giá trị bằng
Cho hàm số . Biết đồ thị hàm số nhận trục hoành và trục tung làm tiệm cận ngang và tiệm cận đứng. Khi đó tổng bằng
Gọi n, d lần lượt là số đường tiệm cận ngang và số đường tiệm cận đứng của đồ thị hàm số . Giá trị của n, d là
Tất cả các giá trị thực của tham số m để đồ thị hàm số có tiệm cận ngang là
Cho hàm số với . , . Hàm số có đồ thị như hình vẽ bên dưới.
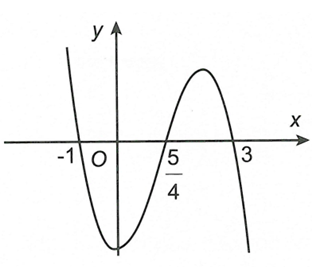
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số có hai tiệm cận đứng?