Trong ngày hội giao lưu văn hóa – văn nghệ, giải cầu lông đơn nữ có 12 vận động viên tham gia, trong đó có hai vận động viên Kim và Liên. Các vận động viên được chia làm hai bảng A và B mỗi bảng gồm 6 người. Việc chia bảng được thực hiện bằng cách bốc thăm ngẫu nhiên. Tính xác suất để haivận động viên Kim và Liên thi đấu chung một bảng.

Phương trình tiếp tuyến của đồ thị hàm số $y=\frac{x+1}{x-2}$ tại điểm có hoành độ bằng 1 là

Cho hàm số y= f(x) có bảng xét dấu đạo hàm như sau:

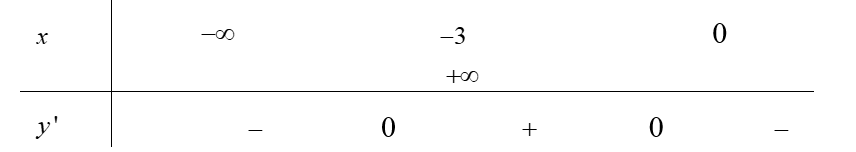
Hàm số y= f(x) đồng biến trên khoản nào dưới đây?

Tìm công bội q của cấp số nhân $\left(u_n\right)$ biết $u_1=1$ và $u_2=4.$

Cho hình nón có chiều cao bằng 4a và bán kính đáy bằng 3a. Diện tích xung quanh của hình nón là

Số thực a thỏa mãn điều kiện ${\log }_3\left({\log }_{2}a\right)=0$ là

Tập nghiệm của bất phương trình $9^x-2\left(x+5\right){.3}^x+9\left(2x+1\right)\ge 0$ là $S=\left[a;b\right]\cup \left[c;+\infty \right).$ Khi đó a-2b+c bằng:

Gọi S là tập hợp tất cả các giá trị của tham số m sao cho giá trị lớn nhất của hàm số $f\left(x\right)=\left|\frac{x^2+2mx+4m}{x+2}\right|$ trên đoạn $\left[-1;1\right]$ bằng 3. Tích các phần tử của S bằng

Khối đa diện như hình vẽ bên có bao nhiêu mặt?

Tìm tất cả các giá trị thực của tham số m để hàm số $y=mx+\cos x$ đồng biến trên $\mathrm{ℝ}$

Cho hai hàm số: $f\left(x\right)=\frac{1}{3}{x}^3-\left(m+1\right)x^2+\left(3m^2+4m+5\right)x+2021$ và $g\left(x\right)=\left(m^2+2m+5\right)x^3-\left(2m^2+4m+9\right)x^2-3x+2$ với m là tham số. Hỏi phương trình $g\left(f\left(x\right)\right)=0$ có bao nhiêu nghiệm?

Tính thể tích khối cầu có bán kính bằng 3cm

Một chiếc hộp có 9 thẻ được đánh số từ 1 đến 9. Có bao nhiêu cách rút được từ hộp trên 2 thẻ đều đánh số chẵn.

Cho hàm số f(x) có $f\text{'}\left(x\right)=x^{2021}{\left(x-1\right)}^{2020}\left(x+1\right);\forall x\in ℝ.$ Hàm số đã cho có bao nhiêu điểm cực trị?

Trong không gian với hệ tọa độ Oxyz cho ba điểm $A\left(2;-1;1\right),$ $B\left(2;1;0\right)$ và $C\left(1;0;3\right).$ Mệnh đề nào sau đây đúng?

Trong không gian cho tam giác ABC vuông cân tại A. Góc ở đỉnh của hình nón nhận được khi quay tam giác ABC xung quanh trục AB bằng