 Giải bởi Vietjack
Giải bởi Vietjack
Do MEOF là hình chữ nhật vuông tại O.
Có CD là tiếp tuyến của tại M.
Suy ra MO là đường cao của , do đó (hệ thức lượng trong tam giác vuông)
Từ ý a) ta có (không đổi) (đpcm).
Xác định m để (d) cắt hai trục Ox, Oy tại A và B sao cho tam giác AOB có diện tích bằng 2 (đơn vị diện tích).
Xác định m để đường thẳng (d) song song với đường thẳng y=2x+1.
Một cột cờ vuông góc với mặt đất có bóng dài 12m, tia nắng của mặt trời tạo với mặt đất một góc là (hình vẽ bên). Tính chiều cao của cột cờ.

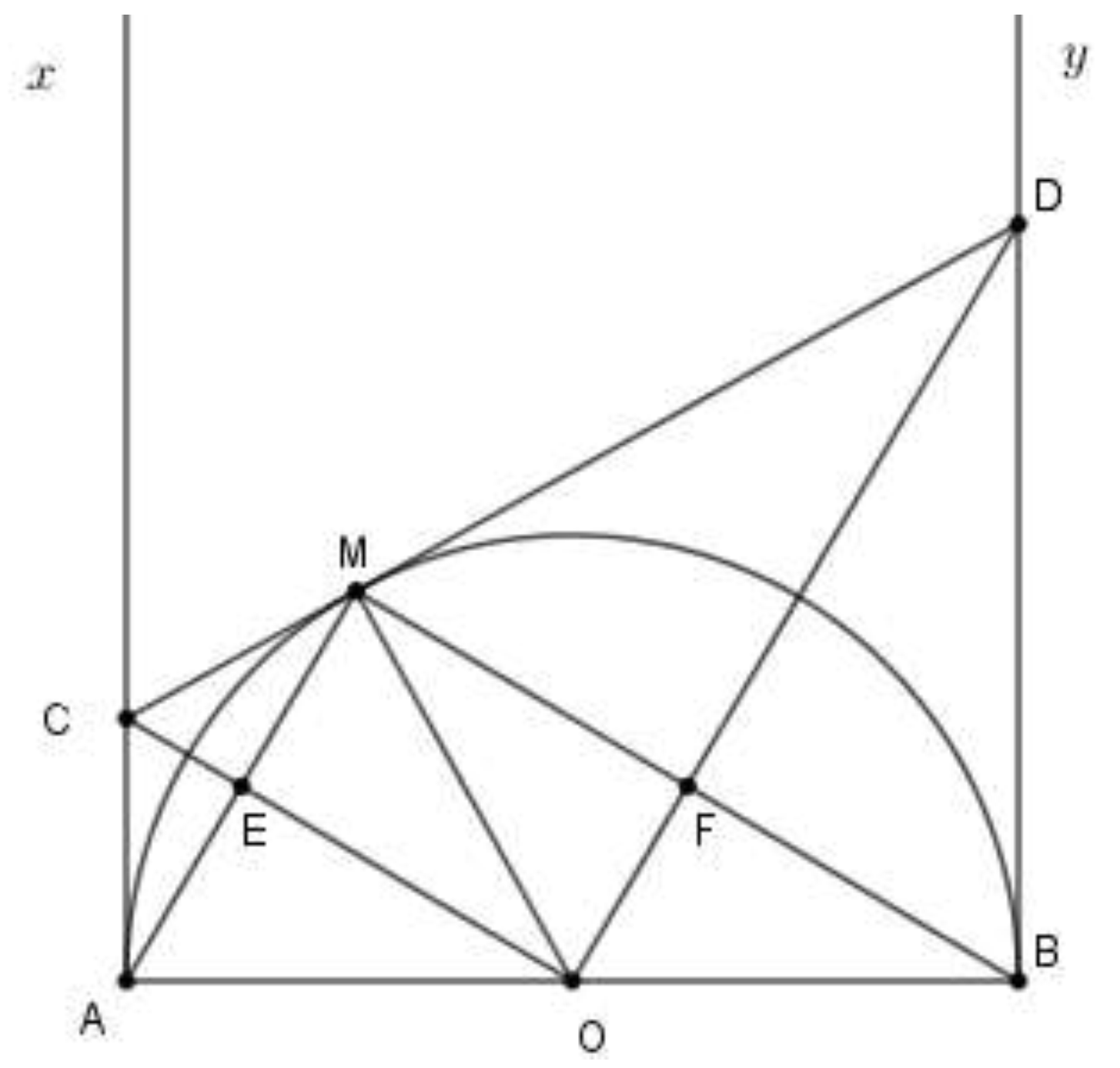
Chứng minh AC+BD=CD và tứ giác MEOF là hình chữ nhật.
Cho nửa đường tròn tâm O, đường kính . Trên nửa mặt phẳng có bờ là AB chứa nửa đường tròn, vẽ tiếp tuyến Ax, By. Từ điểm M tùy ý thuộc đường tròn (M khác A, B) vẽ tiếp tuyến tại M cắt Ax, By lần lượt tại C, D. Gọi E là giao điểm của CO và AM, F là giao điểm của DO và BM.
Chứng minh 4 điểm A, C, M, O cùng thuộc một đường tròn.
Cho các biểu thức ; (với )
Tính giá trị của biểu thức A khi x=36.