Một chiếc hộp hình hộp chữ nhật ABCD.FEGH, mặt trên EFGH không có nắp (xem hình bên).
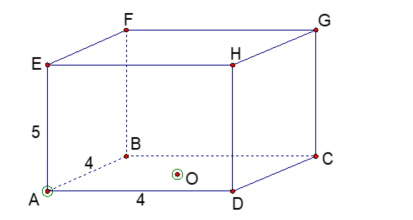
Có một con kiến ở đỉnh A bên ngoài hộp và một miếng mồi của kiến tại điểm O là tâm đáy ABCD ở bên trong hộp. Tính quãng đường ngắn nhất mà con kiến tìm đến miếng mồi (làm tròn đến một chữ số thập phân).
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C.
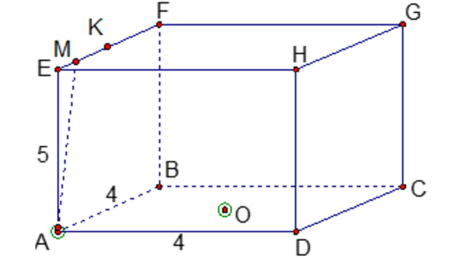
( Hình 1)
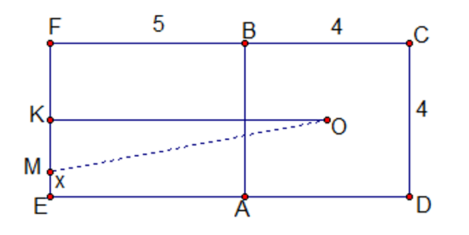
( Hình 2)
Đầu tiên kiến bò đến điểm M trên miệng hộp ( M thuộc đoạn EK với K là trung điểm EF )
( cạnh EF và EH là như nhau – với mỗi điểm M thuộc đoạn EK, có điểm M* thuộc đoạn KF sao cho MO = M*O ). Tiếp tục kiến thực hiện quãng đường ngắn nhất ( bên trong hộp ) từ M đến O- lúc này ta trải hai hình chữ nhật EFBA và ABCD lên mặt phẳng.
Gọi EM =x, 0 x 2 và S là quãng đường ( ngắn nhất) mà kiến thực hiện.
S = AM +MO
Trên hình 1 thì , trên hình 2 ( hình khai triển) thì MO =
Ta có:
( chú ý là bất đẳng thức
Dấu = xảy ra khi .
Gọi a là số thực, a > 1 sao cho phương trình có nghiệm duy nhất. Chọn mệnh đề đúng.
Cho khối chóp tứ giác đều nội tiếp trong khối cầu có bán kính bằng R=9. Tính chiều cao h của khối chóp để thể tích khối chóp lớn nhất.
Tính diện tích xung quanh hình trụ biết hình trụ có đường kính đáy là 2a và đường cao là .
Đường cong trong hình vẽ bên là đồ thị của hàm số có dạng
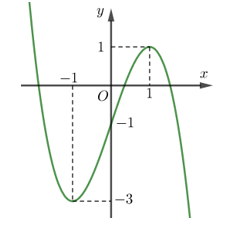
Hàm số đồng biến trên khoảng nào dưới đây?
Xếp ngẫu nhiên 6 học sinh nam và 3 học sinh nữ thành một hàng ngang. Tính xác suất để có đúng 2 học sinh nam đứng xen kẽ với 3 học sinh nữ.
Gọi l,h,r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích xung quanh của hình nón là:
Hai xạ thủ bắn mỗi người một viên đạn vào bia một cách độc lập. Biết xác xuất trúng của xạ thủ thứ nhất và xạ thủ thứ hai lần lượt là 0,9 và 0,7 .Xác suất để có ít nhất một xạ thủ bắn trùng bia là
Gọi m,n lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên Tính m + n.
Cho hình nón đỉnh S đáy là đường tròn tâm O bán kính R= 5, góc ở đỉnh bằng
Cho hình chóp S.ABC có đáy ABC là tam giác đều, và SA tạo với mặt đáy góc Tính thể tích khối chóp S.ABC .
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc và AB= a, , . Khoảng cách d từ điểm A đến mặt phẳng (BCD) là
Cho 2 số thực x,y với . Biết biểu thức có giá trị nhỏ nhất là với a,b là các số nguyên dương và là phân số tối giản. Tính .
Có bao nhiêu mặt phẳng cách đều tất cả các đỉnh của một hình lăng trụ tam giác?