Gọi M và m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = 2{\sin ^2}x - \cos \,x + 1\). Thể thì M.m bằng:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Phương pháp:
Đặt \(\cos \,x = t\). Tìm GTLN, GTNN của hàm số với ẩn là t.
Cách giải:
\(y = 2{\sin ^2}x - \cos \,x + 1 = 2 - 2{\cos ^2}x + 1 = - 2{\cos ^2}x - \cos \,x + 3\)Đặt \(\cos \,x = t,\,\,t \in \left[ { - 1;1} \right]\). Hàm số trở thành: \(y = 2{t^2} - t + 3,\,\,\,y' = - 4t - 1 = 0 \Leftrightarrow t = - \frac{1}{4}\)
Ta có: \(y\left( { - 1} \right) = 2,\,\,\,y\left( { - \frac{1}{4}} \right) = \frac{{25}}{8},\,\,\,y\left( 1 \right) = 0\)
\( \Rightarrow \min y = 0 = m,\,\,\,\max y = \frac{{25}}{8} = M \Rightarrow M.m = 0\)
Giả sử A và B là các giao điểm của đường cong \(y = {x^3} - 3x + 2\) và trục hoành. Tính độ dài đoạn thẳng AB:
Cho hình chóp S.ABC có \(SA = a,\,\,SB = b,\,\,SC = c\) và \(ASB = BSC = CSA = {60^0}\). Tính thể tích của khối chóp S.ABC.
Giá trị nhỏ nhất của số thực m để hàm số \(y = \frac{1}{3}{x^3} + m{x^2} - mx - m\) đồng biến trên \(\mathbb{R}\) là:
Cho khối chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\); tam giác ABC vuông tại A, biết \(BC = 3a;\,\,\,AB = a\). Góc giữa mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) bằng \({45^0}\). Tính thể tích khối chóp S.ABC theo a.
Cho bất phương trình \({\log _{\frac{1}{5}}}f\left( x \right) > {\log _{\frac{1}{5}}}g\left( x \right)\). Khi đó, bất phương trình tương đương:
Điều kiện cần và đủ của tham số m để hàm số \(y = {x^3} - {x^2} + mx - 5\) có cực trị là:
Phương trình \({3^{2x + 1}} - {4.3^x} \({x_1},\,{x_2}\) trong đó \({x_1} < {x_2}\), chọn phát biểu đúng.
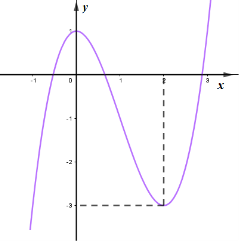
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị trong hình bên. Hỏi phương trình \(y = a{x^3} + b{x^2} + cx + 2 = 0\) có bao nhiêu nghiệm?
Tập xác định của hàm số \(y = {\log _2}\frac{{x + 3}}{{2 - x}}\) là:
Cho hàm số \(y = {x^3} - 2m{x^2} + 1\) có đồ thị \(\left( {{C_m}} \right)\). Tìm m sao cho \(\left( {{C_m}} \right)\) cắt đường thẳng \(d:y = x + 1\) tại ba điểm phân biệt có hoành độ \({x_1},\,{x_2},\,{x_3}\) thỏa mãn \({x_1} + {x_2} + {x_3} = 101\)
Giá trị lớn nhất của hàm số \(f\left( x \right) = \frac{{mx - 1}}{{2x + m}}\) trên đoạn \(\left[ {3;5} \right]\) bằng 2 khi và chỉ khi: