Cho hình chóp SABCD , có đáy ABCD là hình thang vuông tại A và D , có AB= 2a , AD=DC=a , SA=a và . của góc giữa hai mặt phẳng (SBC) và là
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Gọi I là trung điểm của AB suy ra .
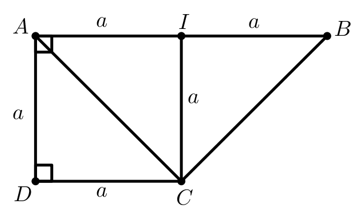
Suy ra (1).
Mà (2)
Từ (1) và (2) suy ra
Vậy góc giữa hai mặt phẳng (SBC) và (iABCD) là góc giữa hai đường thẳng trong hai mặt phẳng cùng vuông góc với giao tuyến, tức là góc .
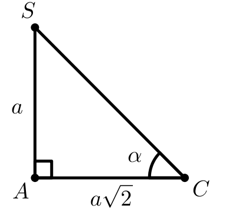
Do đó .
Cho hình chóp SABC có đáy ABC là tam giác đều cạnh 2a , hai mặt bên (SAB) và (SAC) cùng vuông góc với đáy. Góc giữa cạnh bên SB và mặt phẳng (ABC) là . Tính thể tích V khối chóp SABC .
Cho lăng trụ tam giác đều ABCA'B'C' có AB=a ; A'B tạo với mặt đáy (ABC) một góc 60 . Tính thể tích V khối lăng trụ đã cho.
Kí hiệu m,M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số trên đoạn . Tính giá trị của biểu thức .
Cho hình chóp SABC có đáy là tam giác vuông cân tại C , cạnh huyền có độ dài bằng 8a . Gọi M là trung điểm của BC , hình chiếu vuông góc của S xuống mặt phẳng (ABC) là trung điểm H của AM và . Khoảng cách từ đến mặt phẳng (ABC) là:
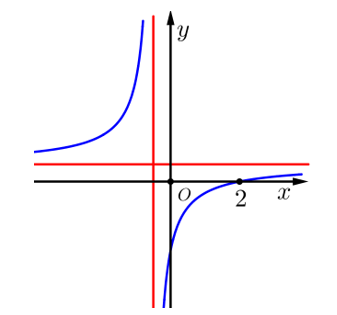
Tìm tất cả các giá trị thực của tham số m sao cho hàm số giảm trên các khoảng xác định của nó?