Cho hình chóp S.ABCD có đáy ABCD là hình bình hành thỏa mãn \(AB = a,\,\,AC = a\sqrt 3 ,\,\,BC = 2a\). Biết tam giác SBC cân tại S, tam giác SCD vuông tại C và khoảng cách từ D đến mặt phẳng \(\left( {SBC} \right)\) bằng \(\frac{{a\sqrt 3 }}{3}\). Tính thể tích V của khối chóp đã cho.
D. \(V = \frac{{{a^3}}}{{\sqrt 5 }}\)
Giải bởi Vietjack
Đáp án A
Phương pháp:
+) Chứng minh \(AB \bot \left( {SAC} \right) \Rightarrow {V_{S.ABC}} = {V_{B.SAC}} = \frac{1}{3}AB.{S_{\Delta SAC}}\)
+) \(AD//BC \Rightarrow d\left( {D;\left( {SBC} \right)} \right) = d\left( {A;\left( {SBC} \right)} \right)\)
+) Dựng \(AE \bot SC\), tính AE.
+) Tính \(\cos \,C\) của tam giác SBC, từ đó tính SC, tính \({S_{\Delta SAC}} = \frac{1}{2}AE.SC\)
Cách giải:
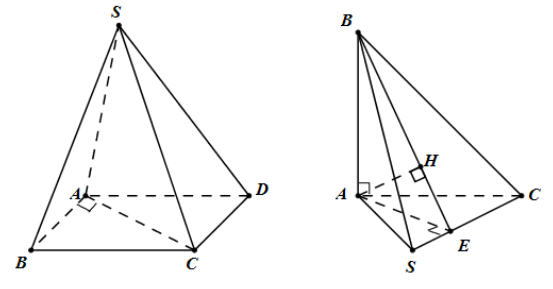
Ta có: \(A{B^2} + A{C^2} = {a^2} + 3{a^2} = 4{a^2} = B{C^2} \Rightarrow \Delta ABC\) vuông tại A (Định lí Pytago đảo)
\( \Rightarrow AB \bot AC \Rightarrow CD \bot AC\,\,\,\left( 1 \right)\)
Mà \(CD \bot SC\,\,\left( 2 \right)\) (\(\Delta SCD\)vuông tại C)
Từ (1) và (2) \( \Rightarrow CD \bot \left( {SAC} \right) \Rightarrow AB \bot \left( {SAC} \right)\)
Ta có: \(AD//BC \Rightarrow AD//\left( {SBC} \right) \Rightarrow d\left( {D;\left( {SBC} \right)} \right) = d\left( {A;\left( {SBC} \right)} \right)\)
Dựng \(AE \bot SC\) tại E, \(AH \bot BE\) tại H ta có \(d\left( {A;\left( {SBC} \right)} \right) = AH = \frac{{a\sqrt 3 }}{3}\)
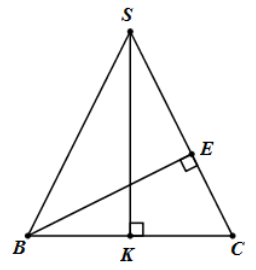
\(BE = \sqrt {{a^2} + \frac{{{a^2}}}{2}} = \frac{{a\sqrt 6 }}{2}\)
Xét tam giác vuông BCE: \(\sin C = \frac{{BE}}{{BC}} = \frac{{\frac{{a\sqrt 6 }}{2}}}{{2a}} = \frac{{\sqrt 6 }}{a} \Rightarrow \cos \,C = \frac{{\sqrt {10} }}{4}\)
Áp dụng định lí cosin ta có:
\(\cos \,C = \frac{{B{C^2} + S{C^2} - S{B^2}}}{{2BC.SC}} = \frac{{B{C^2}}}{{2.BC.SC}} = \frac{{BC}}{{2SC}}\)
\( \Rightarrow \frac{{\sqrt {10} }}{4} = \frac{{2a}}{{2SC}} \Leftrightarrow SC = \frac{{4a}}{{\sqrt {10} }}\)
\( \Rightarrow {S_{\Delta SAC}} = \frac{1}{2}AE.SC = \frac{1}{2}.\frac{a}{{\sqrt 2 }}.\frac{{4a}}{{\sqrt {10} }} = \frac{{{a^2}\sqrt 5 }}{5}\)
\( \Rightarrow {V_{S.ABC}} = \frac{1}{3}AB.{S_{\Delta SAC}} = \frac{1}{3}.a.\frac{{{a^2}\sqrt 5 }}{5} = \frac{{{a^3}\sqrt 5 }}{{15}} \Rightarrow {V_{S.ABCD}} = 2{V_{S.ABC}} = \frac{{2{a^3}\sqrt 5 }}{{15}} = \frac{{2{a^3}}}{{3\sqrt 5 }}\)
Cho số phức z và w thỏa mãn \(z + {\rm{w}} = 3 + 4i\) và \(\left| {z - {\rm{w}}} \right| = 9\). Tìm giá trị lớn nhất của biểu thức \(T = \left| z \right| + \left| {\rm{w}} \right|\)
Tìm tham số m để phương trình \({\log _{\sqrt {2018} }}\left( {x - 2} \right) = {\log _{2018}}\left( {mx} \right)\) có nghiệm thực duy nhất.
Trong mặt phẳng phức, gọi A, B, C, D lần lượt là các điểm biểu diễn các số phức \({z_1} = - 1 + i\), \({z_2} = 1 + 2i,\,\,{z_2} = 2 - i,\,\,{z_4} = - 3i\). Gọi S diện tích tứ giác ABCD. Tính S.
Một tổ có 6 học sinh nam và 9 học sinh nữ. Hỏi có bao nhiêu cách chọn 6 học sinh đi lao động, trong đó 2 học sinh nam?
Cho hàm số \(y = x{\mathop{\rm lnx}\nolimits} \). Chọn khẳng định sai trong số các khẳng định sau:
Có bao nhiêu loại khối đa điện đều mà mỗi mặt của nó là một tam giác đều?
Cho số phức z thỏa mãn \(z + 4\overline z = 7 + i\left( {z - 7} \right)\). Khi đó, môđun của z bằng bao nhiêu?
Cho \(\int\limits_{ - 1}^5 {f\left( x \right)dx} = 4\). Tính \(I = \int\limits_{ - 1}^2 {f\left( {2x + 1} \right)dx} \)
Cho hình phẳng D giới hạn bởi đường cong \(y = \sqrt {2 + \cos \,x} \), trục hoành và các đường thẳng \(x = 0,\,\,x = \frac{\pi }{2}\). Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ?
Tìm giá trị lớn nhất của hàm số \(f\left( x \right) = {x^3} - 3{x^2} - 9x + 10\) trên \(\left[ { - 2;2} \right]\)
Cho một đa giác đều 2n đỉnh \(\left( {n \ge 2,\,\,n \in N} \right)\). Tìm n biết số hình chữ nhật được tạo ra từ bốn đỉnh trong số 2n đỉnh của đa giác đó là 45.
Cho các chữ số 0, 1, 2, 3, 4, 5 . Từ các chữ số đã cho lập được bao nhiêu số tự nhiên chẵn có 4 chữ số và các chữ số đôi một bất kỳ khác nhau.
