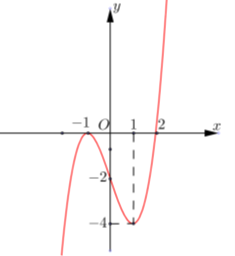
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên R và có đồ thị của hàm \(y = f'\left( x \right)\) như hình vẽ. Xét hàm số \(g\left( x \right) = f\left( {2 - {x^2}} \right)\). Mệnh đề nào dưới đây đúng ?
B. Hàm số \(f\left( x \right)\) nghịch biến trên \(\left( { - \infty ;2} \right)\)
C. Hàm số \(g\left( x \right)\) đồng biến trên \(\left( {2; + \infty } \right)\)
D. Hàm số \(g\left( x \right)\) nghịch biến trên \(\left( { - 1;0} \right)\)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Phương pháp:
Tính đạo hàm của hàm số g(x) và tìm các điểm cực trị, các khoảng đơn điệu của hàm số.
Sử dụng công thức tính đạo hàm của hàm hợp \(\left[ {f\left( {u\left( x \right)} \right)} \right]' = f'\left( u \right).u'\left( x \right)\)
Cách giải:
\(g'\left( x \right) = - 2x.f'\left( {2 - {x^2}} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\f'\left( {2 - {x^2}} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\2 - {x^2} = - 1\\2 - {x^2} = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 3 \end{array} \right.\)
Do đó đáp án A sai.
Với \(x \in \left( { - \infty ;2} \right)\) ta có \(2 - {x^2} \in \left( { - \infty ; - 2} \right) \Rightarrow f'\left( {2 - {x^2}} \right) < 0\), tuy nhiên \(g'\left( x \right) = - 2x.f'\left( {2 - {x^2}} \right)\), chưa kết luận được dấu của \(g'\left( x \right)\) trên \(\left( { - \infty ;2} \right) \Rightarrow \) B sai.
Với \(x \in \left( {2; + \infty } \right) \Rightarrow 2 - {x^2} \in \left( { - \infty ; - 2} \right) \Rightarrow f'\left( {2 - {x^2}} \right) < 0\), tuy nhiên \(g'\left( x \right) = - 2x.f'\left( {2 - {x^2}} \right)\), chưa kết luận được dấu của \(g'\left( x \right)\) trên \(\left( {2; + \infty } \right) \Rightarrow \) C sai.
Với \(x \in \left( { - 1;0} \right) \Rightarrow 2 - {x^2} \in \left( {1;2} \right) \Rightarrow f'\left( {2 - {x^2}} \right) < 0\)
\(x \in \left( { - 1;0} \right) \Rightarrow x < 0 \Rightarrow g'\left( x \right) = - 2xf'\left( {2 - {x^2}} \right) < 0 \Rightarrow \) Hàm số \(g\left( x \right)\) nghịch biến trên \(\left( { - 1;0} \right) \Rightarrow \) D đúng
Cho số phức z và w thỏa mãn \(z + {\rm{w}} = 3 + 4i\) và \(\left| {z - {\rm{w}}} \right| = 9\). Tìm giá trị lớn nhất của biểu thức \(T = \left| z \right| + \left| {\rm{w}} \right|\)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành thỏa mãn \(AB = a,\,\,AC = a\sqrt 3 ,\,\,BC = 2a\). Biết tam giác SBC cân tại S, tam giác SCD vuông tại C và khoảng cách từ D đến mặt phẳng \(\left( {SBC} \right)\) bằng \(\frac{{a\sqrt 3 }}{3}\). Tính thể tích V của khối chóp đã cho.
Tìm tham số m để phương trình \({\log _{\sqrt {2018} }}\left( {x - 2} \right) = {\log _{2018}}\left( {mx} \right)\) có nghiệm thực duy nhất.
Trong mặt phẳng phức, gọi A, B, C, D lần lượt là các điểm biểu diễn các số phức \({z_1} = - 1 + i\), \({z_2} = 1 + 2i,\,\,{z_2} = 2 - i,\,\,{z_4} = - 3i\). Gọi S diện tích tứ giác ABCD. Tính S.
Một tổ có 6 học sinh nam và 9 học sinh nữ. Hỏi có bao nhiêu cách chọn 6 học sinh đi lao động, trong đó 2 học sinh nam?
Cho hàm số \(y = x{\mathop{\rm lnx}\nolimits} \). Chọn khẳng định sai trong số các khẳng định sau:
Có bao nhiêu loại khối đa điện đều mà mỗi mặt của nó là một tam giác đều?
Cho số phức z thỏa mãn \(z + 4\overline z = 7 + i\left( {z - 7} \right)\). Khi đó, môđun của z bằng bao nhiêu?
Cho \(\int\limits_{ - 1}^5 {f\left( x \right)dx} = 4\). Tính \(I = \int\limits_{ - 1}^2 {f\left( {2x + 1} \right)dx} \)
Tìm giá trị lớn nhất của hàm số \(f\left( x \right) = {x^3} - 3{x^2} - 9x + 10\) trên \(\left[ { - 2;2} \right]\)
Cho hình phẳng D giới hạn bởi đường cong \(y = \sqrt {2 + \cos \,x} \), trục hoành và các đường thẳng \(x = 0,\,\,x = \frac{\pi }{2}\). Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ?
Cho tam giác ABC vuông tại A, \(AB = 6cm,\,\,AC = 8cm\). Gọi \({V_1}\) là thể tích khối nón tạo thành khi quay tam giác ABC quanh cạnh AB và \({V_2}\) là thể tích khối nón tạo thành khi quay tam giác ABC quanh cạnh AC. Khi đó, tỷ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng: