Trong không gian Oxyz, cho mặt cầu . Khi đó (S) có tâm I và bán kính R lần lượt là
A. .
B. .
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A
Ta có: .
Vậy (S) có tâm bán kính .
Một hình chữ nhật nội tiếp trong nửa đường tròn bán kính R= 6cm , biết một cạnh của hình chữ nhật nằm dọc theo đường kính của đường tròn mà hình chữ nhật đó nội tiếp. Tính diện tích lớn nhất của hình chữ nhật đó.
Cho tam giác OAB đều cạnh 2a. Trên đường thẳng d qua O và vuông góc với mặt phẳng (OAB) lấy điểm M sao cho . Gọi E,F lần lượt là hình chiếu vuông góc của A trên MB và OB. Gọi N là giao điểm của EF và d. Tìm x để thể tích tứ diện ABMN có giá trị nhỏ nhất.
Cho hình trụ có bán kính bằng 3a. Cắt hình trụ bởi mặt phẳng (P) song song với trục của hình trụ và cách trục của hình trụ một khoảng , ta được một thiết diện là một hình vuông. Tính thể tích của khối trụ đã cho.
Trong không gian Oxyz cho điểm . Tìm tọa độ N đối xứng với M qua trục Oy .
Cho hàm số bậc ba y= f(x) có đồ thị như hình vẽ.
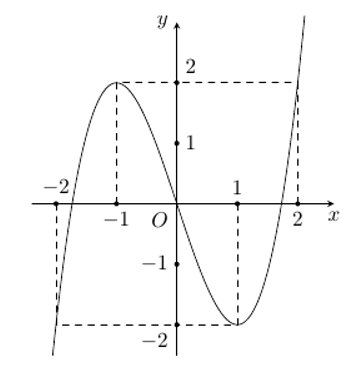
Có bao nhiêu giá trị nguyên của tham số m sao cho phương trình
có nghiệm
Cho hàm số y= f(x) xác định trên và có đạo hàm . Tìm số điểm cực trị của hàm số đã cho.
Cho hàm số có bảng biến thiên dưới đây
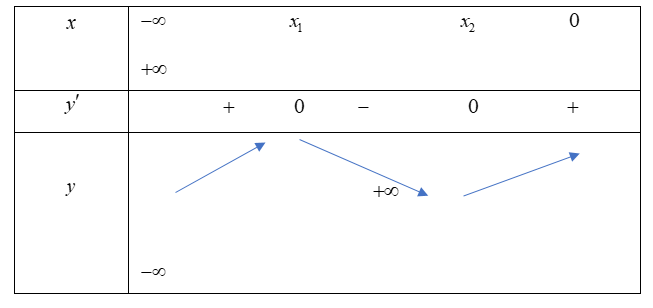
Có bao nhiêu số dương trong các số a, b, c?
Cho đa thức f(x) với hệ số thực và thỏa mãn điều kiện , . Biết tiếp tuyến tại điểm có hoành độ x=1 của đồ thị hàm số tạo với hai trục tọa độ một tam giác. Tính diện tích tam giác đó.
Cho khối chóp có diện tích đáy và chiều cao h=6a. Thể tích khối chóp đã cho bằng
Cho mặt cầu S (O;4) cố định. Hình nón (N) gọi là nội tiếp mặt cầu S(O;4) nếu hình nón (N) có đường tròn đáy và đỉnh thuộc mặt cầu S( O;4). Tính bán kính đáy r của (N) để khối nón (N) có thể tích lớn nhất ?
Cho khối nón có độ dài đường sinh bằng 2a, góc giữa đường sinh và mặt phẳng đáy bằng . Thể tích của khối nón đã cho là
Gọi S là tập hợp các số tự nhiên có 8 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số trong tập S. Tính xác suất để số
được chọn có đúng bốn chữ số lẻ và chữ số 0 có hai chữ số kề nó là chữ số lẻ.