 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ.
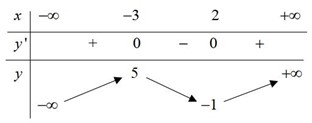
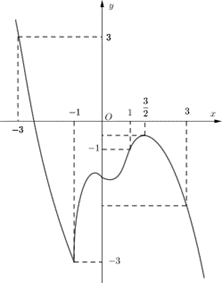
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 2;6} \right]\) và có đồ thị như hình vẽ.
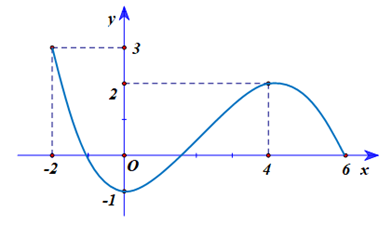
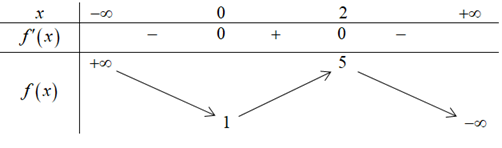
Giá trị cực tiểu của hàm số đã cho bằng