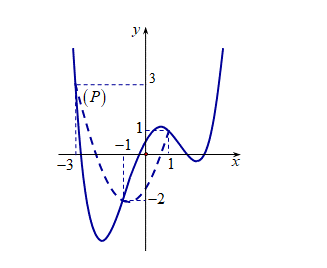Lời giải
Chọn A
Ta có: \(g\left( x \right) = f\left( x \right) - \frac{1}{3}{x^3} - \frac{3}{4}{x^2} + \frac{3}{2}x + 2018 \Rightarrow g'\left( x \right) = f'\left( x \right) - {x^2} - \frac{3}{2}x + \frac{3}{2}\)
+ \(g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = {x^2} + \frac{3}{2}x - \frac{3}{2}\). Đặt \(y = {x^2} + \frac{3}{2}x - \frac{3}{2}\)có đồ thị (P)
Dựa vào đồ thị \(y = f'\left( x \right)\), ta có: \(\left\{ {\begin{array}{*{20}{c}}{f'\left( { - 1} \right) = - 2}\\{f'\left( 1 \right) = 1}\\{f'\left( { - 3} \right) = 3}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{g'\left( { - 1} \right) = 0}\\{g'\left( 1 \right) = 0}\\{g'\left( { - 3} \right) = 0}\end{array}} \right.\)
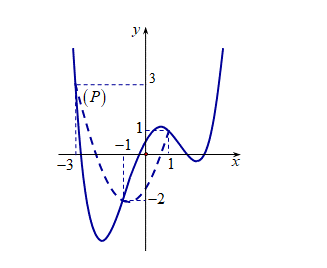
Vẽ đồ thị \(\left( P \right)\)của hàm số \(y = {x^2} + \frac{3}{2}x - \frac{3}{2}\)trên cùng hệ trục tọa độ như hình vẽ trên (đường nét đứt), Đồ thị \(\left( P \right)\)đi qua các điểm \(\left( { - 3;3} \right)\), \(\left( { - 1; - 2} \right)\), \(\left( {1;1} \right)\)với đỉnh \(I\left( { - \frac{3}{4}; - \frac{{33}}{{16}}} \right)\).
Ta thấy: + Trên khoảng \(\left( { - 1;1} \right)\)thì \(f'\left( x \right) > {x^2} + \frac{3}{2}x - \frac{3}{2}\), nên \(g'\left( x \right) > 0\;\;\forall x \in \left( { - 1;1} \right)\)
+Trên khoảng \(\left( { - 3; - 1} \right)\)thì \(f'\left( x \right) < {x^2} + \frac{3}{2}x - \frac{3}{2}\), nên \(g'\left( x \right) < 0\;\;\forall x \in \left( { - 3; - 1} \right)\)
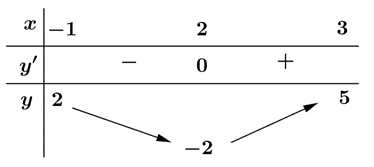
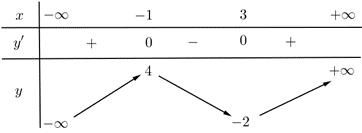
Từ những nhận xét trên, ta có bảng biến thiên của hàm \(y = g'\left( x \right)\)trên \(\left[ { - 3;1} \right]\)như sau:
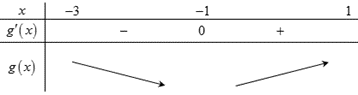
Vậy hàm số \(g\left( x \right)\)đồng biến trên \(\left( { - 1;1} \right)\). Chọn A
Giải bởi Vietjack
để hàm số\[y = \left( {m + 1} \right){x^4} + \left( {m - 3} \right){x^2} + 5{m^2} + 2\] có đúng một điểm cực trị và đồng thời điểm đó là điểm cực đại?
